Areas of Two Similar Triangles:
Theorem 1: Prove that the ratio of the areas of two similar triangles is equal to the ratio of the square of any two corresponding sides.
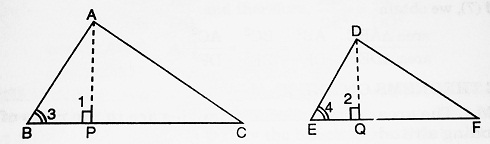
| Given: △ABC ~ △DEF So, AB/DE = BC/EF = AC/DF Also, ∠A = ∠D, ∠B = ∠E, ∠C = ∠F To prove: area △ABC/area △DEF = AB2/DE2 = BC2/EF2 = AC2/DF2 Construction: Through A draw AP ⊥ BC and through D draw DQ ⊥ EF. Proof: area (△ABC) = (1/2) BC x AP; area (△DEF) = (1/2) EF x DQ. Thus, area △ABC/area △DEF = [(1/2) BC x AP]/[(1/2) EF x DQ] ⇒ area △ABC/area △DEF = (BC/EF) x (AP/DQ) ……….(i) In △APB and △DQE, ∠1 = ∠2 = 90° [By construction] ∠3 = ∠4 [given] ∴ △APB ~ △DQE [AA corollary] ∴ AB/DE = AP/DQ = BP/EQ ⇒ AB/DE = AP/DQ ……….(ii) Also, AB/DE = BC/EF [given] ……….(iii) From (ii) and (iii), we get AP/DQ = BC/EF ……….(iv) Putting the value of AP/DQ from (iv) in (i), we get- area △ABC/area △DEF = (BC/EF) x (BC/EF) = BC2/EF2 ……….(v) Similarly. it can also be proved that area △ABC/area △DEF = AB2/DE2 ……….(vi) and area △ABC/area △DEF = AC2/DF2 ……….(vii) From (v), (vi) and (vii), we obtain area △ABC/area △DEF = AB2/DE2 = BC2/EF2 = AC2/DF2 |
Some More Theorems On Areas:
Theorem 1: The areas of two similar triangles are in the ratio of the squares of the corresponding altitudes.
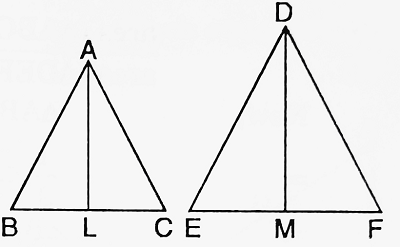
| Given: △ABC ~ △DEF and AL ⊥ BC, DM ⊥ EF To prove: area (△ABC)/area (△DEF) = AL2/DM2 Proof: Since, the ratio of the areas of two similar triangles is equal to the ratio of the squares of any two corresponding sides. ∴ area (△ABC)/area (△DEF) = AB2/DE2 ……….(i) In △ALB and △DME, ∠ALB = ∠DME = 90° and ∠B = ∠E [∵ △ABC ~ △DEF] ∴ △ALB ~ △DME [By AAcorollary] So, AB/DE = AL/DM and therefore, AB2/DE2 = AL2/DM2 ……….(ii) Substituting for AB2/DE2 in (i), we get area (△ABC)/area (△DEF) = AL2/DM2 |
Theorem 2: The areas of two similar triangles are in the ratio of the squares of the corresponding medians.
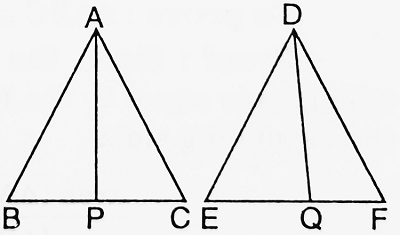
| Given: △ABC ~ △DEF and AP, DQ are their medians. To prove: area (△ABC)/area (△DEF) = AP2/DQ2 Proof: Since, the ratio of the areas of two similar triangles is equal to the ratio of the squares of any two corresponding sides. ∴ area (△ABC)/area (△DEF) = AB2/DE2 ……….(i) Now, △ABC ~ △DEF ⇒ AB/DE = BC/EF = 2BP/2EQ = BP/EQ ……….(ii) Thus, AB/DE = BP/EQ and ∠B = ∠E [∵ △ABC ~ △DEF] ∴ △APB ~ △DQE [By SAS similarity] So, BP/EQ = AP/DQ ……….(iii) From (ii) and (iii), we get AB/DE = AP/DQ and therefore, AB2/DE2 = AP2/DQ2 ……….(iv) ∴ area (△ABC)/area (△DEF) = AP2/DQ2 [from (i) and (iv)] |
Theorem 3: The areas of two similar triangles are in the ratio of the squares of the corresponding angle bisector segments.
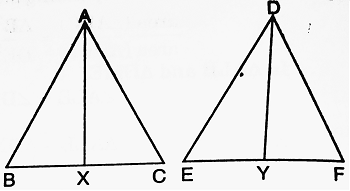
| Given: △ABC ~ △DEF and AX, DY are the bisectors of ∠A and ∠D respectively. To prove: area (△ABC)/area (△DEF) = AX2/DY2 Proof: Since, the ratio of the areas of two similar triangles is equal to the ratio of the squares of any two corresponding sides, we have area (△ABC)/area (△DEF) = AB2/DE2 ……….(i) Now, △ABC ~ △DEF ⇒ ∠A = ∠D ⇒ (1/2) ∠A = (1/2) ∠D ⇒ ∠BAX = ∠EDY ……….(ii) ∴ In △ABX and △DEY, from (ii) ⇒ ∠BAX = ∠EDY and ∠B = ∠E [∵ △ABC ~ △DEF] ∴ △ABX ~ △DEF [By AA corollary] ∴ AB/DE = AX/DY and therefore, AB2/DE2 = AX2/DY2 Substituting AX2/DY2 for AB2/DE2 from (iii) in (i), we get area (△ABC)/area (△DEF) = AX2/DY2 |









Comments (No)