Table of Contents
Trigonometric Functions:
Trigonometric functions are relations between any two of the three sides of a triangle. For the sake of simplicity, a right-angled triangle is taken as a starting point to explain these relations. Among other things, the sides of right-angled triangles are easy to define and grasp. These very ideas will then be extended to all other angles.
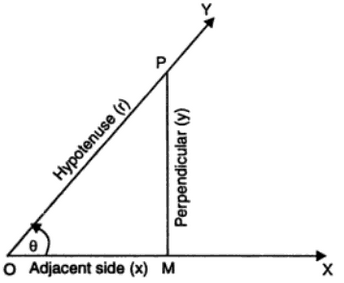
A Right Angle- Let XOY be any angle θ. Take any point P on OY and draw PM perpendicular to OX. A right-angled △OMP is formed. If θ is taken as the angle of reference then MP, the side opposite to θ is called the perpendicular and OP, the side opposite to the right angle is called the hypotenuse and OM, the third side adjacent to the reference angle (other than hypotenuse) is called adjacent side.
Now, the three sides OM, OP and MP can be arranged, two at a time in six different ways and hence six ratios can be formed with them. These six ratios are called the trigonometric functions or circular functions or t-ratios and are defined as follows-
(1) The ratio of the perpendicular to the hypotenuse is called the sine of the angle θ and is written as sin θ.
| sin θ = Perpendicular/Hypotenuse = MP/OP = y/r |
(2) The ratio of the adjacent side or base to the hypotenuse is called the cosine of the angle θ and is written as cos θ.
| cos θ = Adjacent Side or Base/Hypotenuse = OM/OP = x/r |
(3) The ratio of the perpendicular to the adjacent sie or base is called the tangent of the angle θ and is written as tan θ.
| tan θ = Perpendicular/Adjacent Side or Base = MP/OM = y/x |
The following three ratios are reciprocals of the above ratios-
(1) The ratio of the hypotenuse to the perpendicular is called the cosecant of the angle θ and is written as cosec θ.
| cosec θ = Hypotenuse/Perpendicular = OP/MP = r/y |
(2) The ratio of the hypotenuse to the adjacent side or base is called the secant of the angle θ and is written as sec θ.
| sec θ = Hypotenuse/Adjacent Side or Base = OP/OM = r/x |
(3) The ratio of the adjacent side or base to the perpendicular is called the cotangent of the angle θ and is written as cot θ.
| cot θ = Adjacent Side or Base/Perpendicular = OM/MP =x/y |
Relationship Between Trigonometric Ratios:
From the above trigonometric functions, it is clear that cosec θ = 1/sin θ, sec θ = 1/cos θ and cot θ = 1/tan θ. Also, tan θ = sin θ/cos θ.
| Now, in △POM, OM2 + PM2 = OP2 ⇒ x2 + y2 = r2 ⇒ (x/r)2 + (y/r)2 = 1 ⇒ cos2 θ + sin2 θ = 1 …………..(i) Dividing both sides of (i) by cos2 θ, we get- 1 + tan2 θ = sec2 θ …………..(ii) Also, dividing both sides of (i) by sin2 θ, one gets- 1 + cot2 θ = cosec2 θ …………..(iii) |
Concept of Circular Functions with the Help of Unit Circle:

We consider a circle of the unit radius with its centre at O, the origin of the rectangular coordinate system. We denote the point of intersection of OX and the unit circle by A and take a point P on the circle such that arc AP (measured in anticlockwise direction if θ > 0 and in a clockwise direction if θ < 0) subtends an angle |θ| at O. Then, the circular measure of ∠AOP = arc AP/radius = θ/1 = θ.
Let the coordinates of P be (x, y) and PM be dropped perpendicular on the X-axis. Then, OM = x and PM = y. The circular functions of θ are defined as sin θ = y, cos θ = x, tan θ = y/x, cosec θ = 1/y, sec θ = 1/x and cot θ = x/y.
Thus, the circular functions of a real number θ and the trigonometric ratios of ∠AOP are the same.
Domain and Range of Circular Functions:

From the above figure, it is clear that -1 ≤ x ≤ 1 and -1 ≤ y ≤ 1. Again, x > 0, y > 0 in the first quadrant, x < 0, y > 0 in the second quadrant, x < 0, y < 0 in the third quadrant and x > 0, y < 0 in the fourth quadrant.
Thus, in the 1st quadrant, all the six trigonometric ratios are positive. In the 2nd quadrant, x < 0 but y > 0. So, Sin θ = y and cosec θ = 1/y are positive but the remaining four trigonometric ratios are negative.
In the 3rd quadrant, x < 0, y < 0. So, tan θ = y/x and cot θ = x/y are positive but the remaining four t-ratios are negative. Finally, in the 4th quadrant, x > 0, y < 0. So cos θ = x and sec θ = 1/x are positive and the remaining four t-ratios are negative.

The points discussed above may be summarized as follows:
It is clear that sin θ = y and cos θ = x are defined for all real values of θ. But tan θ = y/x and sec θ = 1/x are not defined for x = 0. In this case, OP coincides with the Y-axis and so-
| θ = π/2, 3π/2, 5π/2, … or -π/2, -3π/2, -5π/2, … ⇒ θ = (2n + 1) x/2, where n is any integer. |
Also, cot θ = x/y and cosec θ = 1/y are not defined when y = 0 i.e. when OP coincides with the X-axis. In this case θ = 0, π, 2π, 3π … or -π, -2π, -3π, … ⇒ θ = nπ, where n is any integer.
Again, as -1 ≤ x ≤ 1 and cos θ = x, we have -1 ≤ cos θ ≤ 1. Similarly, -1 ≤ y ≤ 1 and sin θ = y. Therefore, -1 ≤ sin θ ≤ 1. Clearly, the other four trigonometric ratios may have all real values lying between -∞ and ∞.
| I | II | III | IV | |
|---|---|---|---|---|
| sin θ | +ve | +ve | -ve | -ve |
| cos θ | +ve | -ve | -ve | +ve |
| tan θ | +ve | -ve | +ve | -ve |
| cosec θ | +ve | +ve | -ve | -ve |
| sec θ | +ve | -ve | -ve | +ve |
| cot θ | +ve | -ve | +ve | -ve |
| Circular Function | Domain (θ in circular measure) | Range |
|---|---|---|
| sin | all real numbers | (-1, 1) |
| cos | all real numbers | (-1, 1) |
| tan | all real numbers other than (2n +1) π/2, where n is any integer | all real values |
| cosec | all real numbers other than nπ, n being an integer | all real values except -1 and 1 |
| sec | all real numbers other than (2n +1) π/2, n being an integer | all real values except -1 and 1 |
| cot | all real numbers other than nπ, where n is any integer | all real values |









Comments (No)