Table of Contents
Measurement of Angles in Trigonometry:
What is Trigonometry?
The word “Trigonometry” is derived from three Greek words i.e. Trio meaning thrice, Gonia meaning angle and Metron meaning measure. Literally, it means “measurement of triangles i.e., measuring the sides and angles of triangles”. In the study of trigonometry, we generally find remaining sides and angles given some sides and angles of a triangle, whenever possible. The use of trigonometry dates back to the early astronomers, who were concerned with the measurements of angles and distances. It now finds widespread use in navigation and surveying and has many applications in warfare, architecture, engineering, physics and astronomy. This subject found its place in the curriculum of mathematics nearly three centuries ago.
Positive and Negative Angles:
In geometry, angles are always taken in the positive sense and their measures lie between 0° and 360° but in trigonometry, angles may be positive or negative and their measures may have any value.
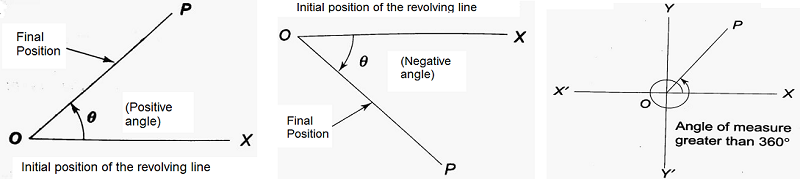
Angles are formed by the revolution of a line segment about a fixed point lying on it starting from a fixed position of the line, known as the initial position. If the line moves in the anticlockwise direction, then the angle formed is regarded as positive, whereas if the revolving line moves in the clockwise direction, then the angle formed is negative. In both cases, if the revolving line after making one complete revolution still continues its revolution, then the measure of the angle is greater than 360°.
Units of Measurement of Angles:
There are three systems of units in which angles are measured. They are-
- Sexagesimal System (also called English System).
- Centesimal System.
- Circular System.
In the sexagesimal system, a right angle is divided into 90 equal parts each of which is called a degree (1°). A degree is again divided into 60 equal parts and each of such parts is known as a minute (1′). One minute is again divided into 60 equal parts each part is known as a second (1”).
| Thus, 1 right angle = 90° 1° = 60′ 1′ = 60” |
In the centesimal system, a right angle is divided into 100 equal parts and each part is called a grade (1g). 1 grade is again divided into 100 equal parts each of which is called a minute (1′). 1 minute is again divided into 100 equal parts, each part being called a second (1”).
| Thus, 1 right angle = 100g 1g = 100′ 1′ = 100” |
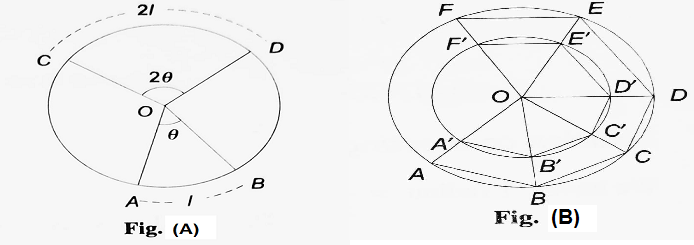
In a circular system, the unit used is called a radian. It is known that in congruent circles or in the same circle the length of an arc is proportional to the angle subtended by it at the centre. Thus, in a circle, if an arc of length ‘l’ subtends an angle ‘θ’ at the centre, then the arc of length 2l will subtend an angle of measure 2θ at the centre (Figure A).
Now, if an angle at the centre is subtended by an arc whose length is equal to the radius of the circle, then the measure of the angle is a radian. 1 circular measure is denoted by 1c. The S.I. symbol for a radian is rad.
We take two concentric circles of different radii. Let ABCDEF ….. be an inscribed regular polygon of n sides. Let A’, B’, C’, D’, E’, F’, be the points of intersection of the radii OA, OB, OC, OD and OE….with the inner circle. Then A’ B’ C’ D’ E’ F’ …….. is another regular polygon of n sides inscribed in the inner circle (Figure B).
Now, in △OAB and △OA’B’, OA = OB (radii of the same circle) and OA’ = OB’ (radii of the same circle).
| ∴ OA/OB = OA’/OB’ ∠AOB = ∠A’OB’ (common) ∴ △OAB ~ △OA’B’ (by SAS similarity) ∴ AB/A’B’ = OA/OA’ ⇒ n.AB/n.A’B’ = OA/OA’ ∴ perimeter of polygon ABCDE…./perimeter of polygon A’B’C’D’E’ = OA/OA’ |
The relation is true for any value of n. So, by making n infinitely large, the perimeters of the polygon can be made coincident with the circumferences of the corresponding circles in which the polygon are inscribed. Thus,
| circumference of the larger circle/circumference of the smaller circle = OA/OA’ = R/r = radius of the larger circle/radius of the smaller circle ⇒ circumference of a circle/radius of the circle = constant |
The constant is denoted by the Greek letter π, whose approximate value has been estimated to be 22/7. In decimal, π = 3.14159 ….
We take a circle with its centre at O. Let AB be an arc of length equal to the radius of the circle. Then, ∠AOB = 1c (Figure C). Now, the angles at the centre of a circle are proportional to the arcs subtending them. Also, the whole angle at O subtended by the circumference is 4 right angles. Thus,
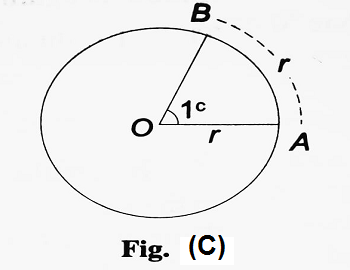
| ∠AOB/4 right angles = radius/circumference = r/π.2r ∴ ∠AOB/4 right angles = 1/2π ∴ ∠AOB = 1/2π . 4 right angles ∴ 1 radian = 2/π right angles = constant Thus, a radian is a constant angle. Also, 1c = 2/π X 90° = 180/π degrees = 57.2958 degrees = 57° 17′ 45” (approx.) ⇒ 1° = 0.017453 radian (approx.) |
Relation Connecting the Units:
| We have, 1 radian = 2/π right angles ∴ 1 right angle = π/2 radian Thus, 1 right angle = 90° = 100g = π/2 radian If we consider the measure of an angle to be D in degrees, G in grades and R in radians, then, D/90 = G/100 = 2R/π |
Length of an Arc of a Circle:
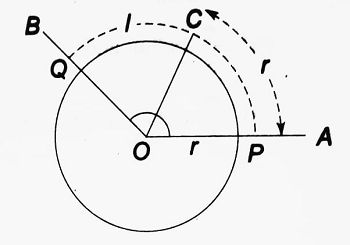
Let ∠AOB be a given angle. With O as a centre and taking r as the radius (on a certain scale), a circle is drawn to cut OA at P and OB at Q respectively. Now, from the arc PQ, PC is cut off such that PC = r.O and C are joined. Let PQ = l.
| Here, the measure of ∠POC = 1 radian. ∴ measure of ∠POQ/measure of ∠POC = PQ/PC = l/r ∴ measure of ∠POQ = l/r measure of ∠POC = l/r X 1 radian = l/r radian If θ be the circular measure of ∠POQ, then θ = l/r ∴ l = rθ Thus, the length of the arc = radius X angle subtended by the arc at the centre |
Area of a Sector of a Circle:
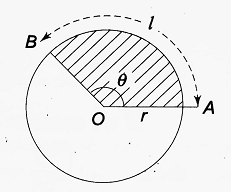
| Let AOB be the sector of a circle of radius r with the centre at O. Also, let ∠AOB = θ and AB =l Then, as the area of a sector is proportional to the angle subtended by it at the centre, we have area of the sector/area of the circle = θ/4 right angles = θ/4.π/2 = θ/2π [∵ 1 right angle = π/2 radians] Now, if A be the area of the sector, then- A/πr2 = θ/2π ∴ A = πr2θ/2π = 1/2 r2θ = 1/2 r2 . l/r = 1/2 rl |









Comments (No)