Cornu’s Method for Determination of Young’s Modulus:
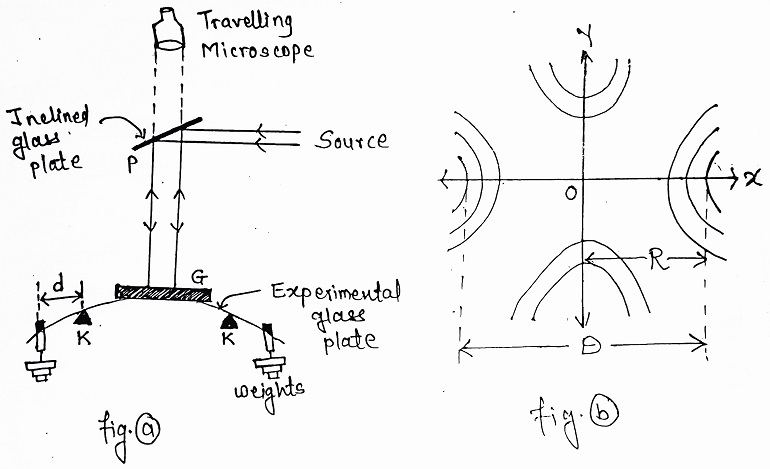
In 1869 Cornu obtained a method for determining the elastic constants of glass by observing the deformations obtained on its surface when subjected to a uniform bending moment. The curvature of the surface was obtained by supporting the plate on two knife edges lying on a horizontal plane with their edges normal to the axis of the plate and suspending weights from the ends.
The given experimental plate is symmetrically placed over the knife edges and the weight hangers are suspended at equal distances ‘d’ from the knife edges. A plane glass plate ‘G’ is placed on the centre of the experimental plate. Light from a sodium lamp is partially reflected to this plate and partially refracted to a microscope by means of another glass plate ‘P’ fixed at 45° inclination in between the plate ‘G’ and the microscope. Suitable weights are added in the weight hangers (equally) and the microscope is focussed to view the hyperbolic fringes. The fringes are formed between the upper surface of the glass plate and the plane glass.
Using a travelling microscope, the diameter D of the fringe in a direction parallel to the longitudinal axis of the glass plate can be measured.
This gives the radius of curvature R. Young’s modulus of the material of the glass plate can be found by using the relation-
| YI/R = M = mgd ……….(i) |
Where ‘I’ is the moment of inertia of a cross-section of the plate about an axis through the centroid and perpendicular to the plane of the plate. It is given by-
| I = ab3/12 |
| Where ‘a’ is the breadth. ‘b’ is the thickness of the plate. ‘R’ is the longitudinal radius of curvature which is obtained from the fringe diameter D. ‘m’ is the load added to the weight hanger. ‘g’ is the acceleration due to gravity. ‘d’ is the distance between knife edge and point of suspension of load. |








