Table of Contents
Applications of Michelson Interferometer:
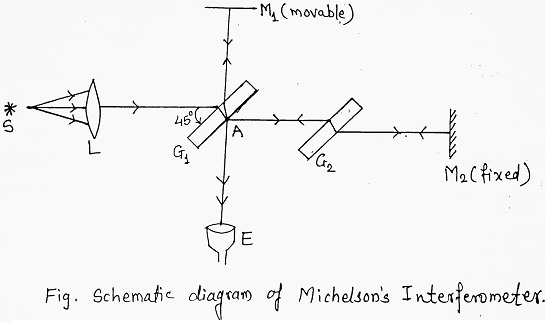
Determination of Wavelength of Monochromatic Light:
When M1 and M2 are perfectly perpendicular to each other then at a certain position of mirror M1 (say x1), circular alternately dark and bright fringes are observed. The effect of moving M1 is to change the thickness of equivalent air film. Suppose at x1 a bright fringe appears at the center. If a mirror is moved such that the next bright fringe appears at center, then it is equivalent to a path difference of λ/2. Thus a large number of fringes are counted, say N, for the position of Mirror ‘x2‘, we can write,
| X = (x2 – x1) = Nλ/2 ∴ λ = 2X/N |
Resolution of Spectral Lines:
Resolution of Spectral Lines (i.e. determination of the difference in wavelength between two neighbouring spectral lines).
Let λ1 and λ2 be the wavelengths of two close spectral lines of Na-light (λ1 > λ2). Then dλ = λ1 – λ2 is called the resolution of lines.
When such light is used in Michelson Interferometer then each spectral line will give rise to its fringes. Mirror M1 is then adjusted to get a clear and distinct fringe pattern which is possible when nth bright fringe due to longer wavelength λ1 coincides with (n + 1)th bright fringe due to shorter wavelength λ2. When M1 is further moved, two sets of fringes get out of step and intensity will be reduced. M1 is still further moved, two sets of fringes get out of step and intensity will be reduced. M1 is still further move through the distance at which due to overlapping of dark with dark and bright to bright, clear and distinct fringe pattern reappears.
Let ‘x’ be the displacement of the mirror during two distinct bright positions, we can write-
| x = nλ1/2 ……….(i) and x = (n + 1) λ2/2 ……….(ii) ⇒ nλ1 = (n + 1) λ2 ⇒ n (λ1 – λ2) = λ2 or n = λ2/(λ1 – λ2) ……….(iii) Using (iii) in (i), we get- 2x = λ1λ2/(λ1 – λ2) or (λ1 – λ2) = λ1λ2/2x or dλ = λ2/2x Where λ is the mean of two wavelengths. |
Determination of Refractive Index of a Thin Transparent Film:
| Let t = thickness of thin transparent plate or film. µ = refractive index of its material. |
The Michelson Interferometer is adjusted to get circular fringes in the field of view of the telescope. By moving M, the vertical cross-wire is so adjusted it coincides with any bright fringe.
Let x1 be the position of mirror M1.
Then looking through the eyepiece, introduce a thin transparent plate in the path of one of the interfering rays (i.e. ray 1 or 2). The bright fringe shifts from its original position. Move the mirror M1 with the micrometer screw till the vertical cross-wire coincides with the original bright fringe. Also, count the number of fringes N crossing the field of view during the shift.
| ∴ Path difference introduced between the rays due to displacement (x2 – x1) of M1 is = 2 (x2 – x1). The path difference introduced between the rays due to the introduction of thin plate is = 2µt – 2t = 2t (µ – 1). Then, 2 (x2 – x1) = 2t (µ – 1) ∴ t = (x2 – x1)/(µ – 1) = x/(µ – 1) = Nλ/2(µ – 1) ……….(i) where x = (x2 – x1) = displacement of M1. Thus by knowing x and µ, t can be calculated. On the other hand, from equation (i) we have- x = (µ – 1) t ∴ µ = x/t + 1 Thus knowing x and t, the refractive index of the material of film can be calculated. |








Comments (No)