Table of Contents
Betatron:
Betatron is a circular particle accelerator to accelerate electrons to extremely high energies up to 300 MeV. It was invented by D. W. Kerst. It is different from cyclotron in two fundamental respects-
- The electrons are accelerated by an expanding magnetic field.
- The circular orbit of the electron has a constant radius.
Betatron Principle:
The principle of betatron is similar to that of the transformer, i.e., it is “mutual induction“. The primary current produces an oscillating magnetic field which, in turn, induces an oscillating potential in the secondary coil.
In betatron, a magnetic field is produced in electro-magnets (i.e. primary coil) while the cloud of electrons, located inside the doughnut-shaped vacuum chamber, takes the place of secondary windings.
The magnetic field has two effects on the electron which is injected into the doughnut,
- Due to changing magnetic flux additional energy is provided to electron i.e. “central flux” (which is due to an electromotive force).
- A radial force (i.e. guide field/lines) is produced by the action of a magnetic field (perpendicular to the velocity of an electron) which keeps the electron in a fixed orbit.
Betatron Construction:
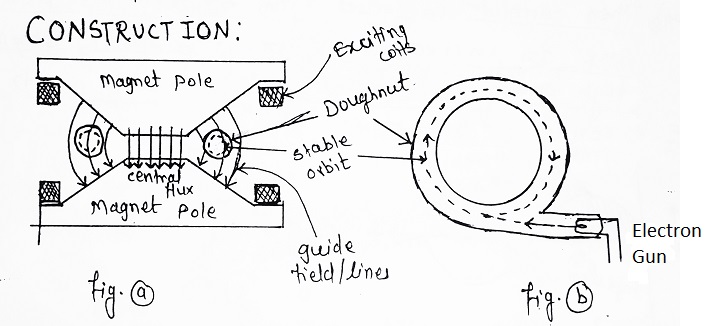
- Doughnut Chamber- It is a specially shaped, highly evacuated glass tube.
- The doughnut chamber is placed between the specially shaped poles of an electromagnet which is excited by an alternating current usually of frequency 80 to 180 Hz. The magnetic field is normal to the plane of the doughnut so that a changing magnetic flux threads the equilibrium orbit.
- The high-velocity electrons from the electron gun are injected into the doughnut when the central main flux is rising in one direction i.e. at the beginning of each cycle.
Betatron Working:
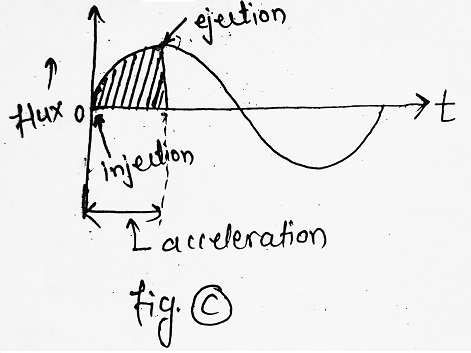
- Electrons from the electron gun are injected into the doughnut chamber when the magnetic field is just rising from its zero value in the 1st quarter cycle (see fig. C).
- As the magnetic field builds up during this part of the cycle, it induces an emf inside the doughnut and accelerates the electrons which are already moving in a circular path by the action of the transverse magnetic field.
- When current increases from zero to its peak value, an increasing flux is suddenly stopped and high-energy electrons leave their path to strike a target.
Betatron Condition:
| Let r be the radius of the circular orbit of an electron which is moving in a doughnut vacuum chamber, under the action of a magnetic field. B = magnetic field at any instant. Φ = total magnetic flux through orbit. The increase in flux due to changing magnetic field is dΦ/dt. ∴ According to Faraday’s Law, emf induced = – dΦ/dt ……….(i) (Whenever there is a change in a magnetic field, an emf is induced in the coil and opposes the magnetic field which produces it). ∴ Work done on an electron in one revolution is, W = charge x emf induced = – e dΦ/dt ……….(ii) Equation (ii) is also called energy gained by electron in one revolution. Work done is also the product of tangential force F acting on the electron and length of the orbit. ∴ W = F x Distance = F x 2πr ……….(iii) i.e. W = – e dΦ/dt = F x 2πr ⇒ F = (- e/2πr) dΦ/dt ……….(iv) This force increases the energy of electron and tends to change the radius ‘r’. Thus to maintain the ‘r’ constant this force must be counterbalanced, which is obtained as follows. For the circular motion of electron, Beν = mν2/r ⇒ mν = Ber ……….(v) According to Newton’s 2nd law, F = d(mν)/dt = d(Ber)/dt = er dB/dt ……….(vi) Thus for ‘r’ to be constant, equations (iv) and (vi) must be numerically equal i.e. (e/2πr) dΦ/dt = er dB/dt ⇒ dΦ/dt = 2πr2 dB/dt or Φ = 2πr2B ……….(vii) This is called the betatron condition, which shows that total flux Φ must be twice the value which would be obtained if B were uniform over the whole area of orbit. Note: (i) Equation (iv) stands for force due to central flux which increases the energy of an electron. (ii) Equation (vi) stands for force due to guide field/lines which keeps radius of electron constant. |
Maximum Energy Gained by Electron (Emax):
| When an electron is accelerated, it acquires a very high speed nearly equal to the velocity of light i.e. ν ≈ c Now we have, Beν = mν2/r ⇒ mν = Ber and Emax = mc2 = mνc = Berc ∴ Emax = Berc ……….(i) Energy gained per revolution = Emax/Total no. of revolutions ……….(ii) and Total no. of revolutions, N = Total distance travelled/Distance travelled in one revolution ⇒ N = (velocity x time)/2πr = (c x t/4)/2πr = (c x 1/4f)/2πr ⇒ N = c/4f x 1/2πr ……….(iii) |









Comments (No)