Table of Contents
What is Mutual Induction?
It is defined as the phenomenon of production of induced EMF in one coil due to the varying current in the neighbouring coil.
Explanation of Mutual Induction:
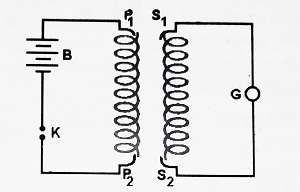
Let us consider two coils P1P2 and S1S2 placed close to each other. The coil P1P2 is connected to a battery B and key K and it is called the primary coil, whereas the coil S1S2 is connected to a galvanometer and it is called a secondary coil.
When the key is pressed, the current in the primary coil increases from zero to maximum and due to this, the magnetic flux linked with the secondary coil also increases from zero to maximum and hence induced EMf is produced in the secondary coil.
When the key is released, the current in the primary coil decreases from maximum to zero value. Hence magnetic flux linked with the secondary coil also decreases from maximum to zero. Hence induced EMF is produced in the secondary coil.
Co-efficient of Mutual Induction or Mutual Inductance:
Let ‘I’ be the current that is flowing through one coil and let ‘Φ’ be the magnetic flux linked with the neighbouring coil. It is found that-
| Φ ∝ I ⇒ Φ = MI ……….(i) |
Where ‘M’ is the constant of proportionality and is called a co-efficient of mutual induction.
| If I = 1, from (i) ⇒ Φ = M |
Thus co-efficient of mutual induction of two coils is numerically equal to the amount of magnetic flux linked with one coil when unit current flows through the neighbouring coil.
| We know, e = -dΦ/dt ……….(ii) Put the value of ‘Φ’ from (i) in (ii), ⇒ e = -d(MI)/dt ⇒ e = -M . dI/dt ……….(iii) If dI/dt = 1, From (iii), e = -M . 1 ⇒ e = M (numerically) |
Thus co-efficient of mutual induction of the two coils is equal to induced EMF produced in one coil when the rate of change of current through the neighbouring coil is unity.
The S.I. unit of co-efficient of mutual induction is Henry.
Definition of Henry:
| We have e = -M . dI/dt If dI/dt = 1Amp/sec and e = 1volt ⇒ M = 1Henry (numerically) |
Thus co-efficient of mutual-induction is said to be 1Henry, when 1 volt EMF is produced in one coil due to one amp/sec rate of change of current in the neighbouring coil.
Mutual Inductance of Two Coaxial Solenoids:
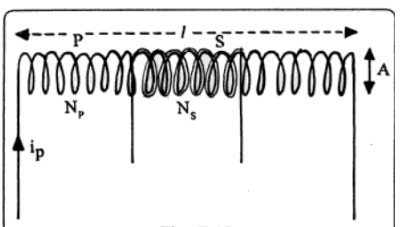
As an example, we consider two coaxial solenoids as shown in the figure. P is a long air-core solenoid of length l and small area of cross-section A. The number of turns in this is NP. Coil S with NS number of turns is wound closely over the central portion of P, insulated from the wire of P. If we send a current IP through coil P, the magnetic field at the axial point inside the long solenoid is given by equation as-
| B = µ0NPIP/l |
Since the area of the cross-section of P is taken small, this value of B may be assumed to be almost constant in the whole cross-section. The flux linked with each turn of P (near the centre of P) is-
| ΦP = B . A = (µ0NPIP/l) . A |
The same flux is linked with each turn of coil S, i.e.,
| ΦS = µ0NPIPA/l |
The total flux linkage with coil S is, therefore-
| NSΦS = (µ0NPNSA/l) . IP But NSΦS = MIP MIP = (µ0NPNSA/l) . IP ⇒ M = µ0NPNSA/l |
This gives the mutual inductance between the pair of coaxial solenoidal coils.
If the core inside the coils is filled with a ferromagnetic material of permeability µ, the mutual inductance becomes-
| M’ = µNPNSA/l Naturally M’ > M (as µ >> 1) |









Comments (No)