Resolving Power of Telescope:
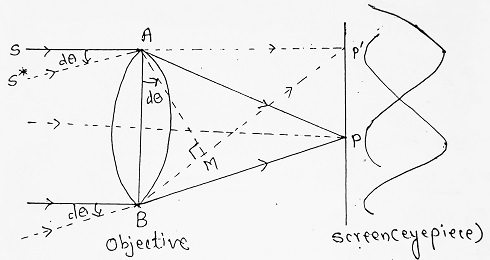
The resolving power of telescope is defined as the reciprocal of the smallest angle subtended at the objective by the two distant point objects (for example- two stars) which can be just seen as separate through the telescope.
(1) Consider two point sources such as two stars S and S* having angular separation ‘dθ’.
(2) Let the parallel beam of light from these sources be made to incident on the objective of the telescope. (The ring supporting the telescope objective and lens itself serve as a circular aperture.
(3) Let P and P’ be the positions of the central maxima of the two images.
(4) The pattern will lie very close to each other with a large amount of overlapping. If the overlapping is too much, the telescope may not be able to distinguish them as separate.
(5) According to Rayleigh’s criterion, the pattern will be just resolved if the central maximum of one falls on the 1st minimum of the other.
(6) The path difference produced between extreme diffracted rays is BM and is given by-
| Path Difference = BM = BP‘ – AP‘ ……….(i) ⇒ Path Difference = AB sin dθ ⇒ Path Difference = AB dθ, (as dθ is small, sin dθ = dθ) ∴ Path Difference = D dθ ……….(ii) Where, D = AB, the diameter of the objective of the telescope. |
The path difference, D dθ is equivalent to λ, i.e. D dθ = λ, the position P’ corresponds to the 1st minimum of the 1st image i.e. S. But it is also the position of the central maximum of the second image i.e. S*.
Thus to satisfy Rayleigh’s criterion, we should write-
| Path Difference = D dθ = λ or dθ = λ/D ……….(iii) |
This equation (iii) holds good for rectangular aperture. According to Airy for circular aperture, this condition can be expressed as-
| dθ = 1.22 λ/D ……….(iv) |
Here ‘dθ’ represents the limit of resolution of the telescope. Reciprocal of dθ measures i.e. R.P. of telescope-
| ∴ R.P. = 1/dθ = D/1.22 λ ……….(v) |
Thus a telescope with a large diameter of objective has a higher resolving power.









Comments (No)