Table of Contents
Enthalpy and Entropy:
What is Enthalpy?
The heat capacity of a system at constant pressure is called enthalpy. It is denoted by symbol H. Mathematically, enthalpy is related to internal energy as-
H = U + PV
In case of gases-
PV = nRT (ideal gas equation)
H = U + nRT
Where, U = internal energy, P = pressure, T = kelvin temperature, R = molar gas constant and V = volume of the system
Components of Enthalpy:
Enthalpy includes all the components of internal energy and in addition, it also includes PV energy i.e. energy consumed in doing PV work.
Characteristics of Enthalpy:
- Enthalpy is an extensive property because it depends upon the amount of substances present in the system. Larger the amount of the substance, larger is the value of H.
- Enthalpy of a system is a state function. It depends upon the state variables (T, P, V, n).
- When a system undergoes a physical or a chemical change, its enthalpy also changes. The change in enthalpy is denoted by ΔH and it is defined as the difference between the enthalpies of the final and initial states of the system i.e. ΔH = Hfinal – Hinitial.
- Enthalpy change is equal to the amount of heat absorbed or liberated in a process at constant temperature and constant pressure i.e. ΔH = qp.
- ΔH is measured by bomb calorimeter, which is open to atmosphere so that volume may change but the pressure remains constant at atmospheric pressure.
- The units of ΔH are Kcal/mole or KJ/mole.
- ΔH is related to ΔU as, ΔH = ΔU + P ΔV. Where ‘P ΔV’ represents a change in volume of the system at constant pressure.
Relation between ΔH and ΔU:
ΔH = ΔU + P ΔV
Also, ΔH = ΔU + Δng RT
What is Entropy?
Entropy is defined as the degree of disorder or randomness in a system. Greater the randomness, larger is the value of entropy. It is denoted by the ‘S‘.
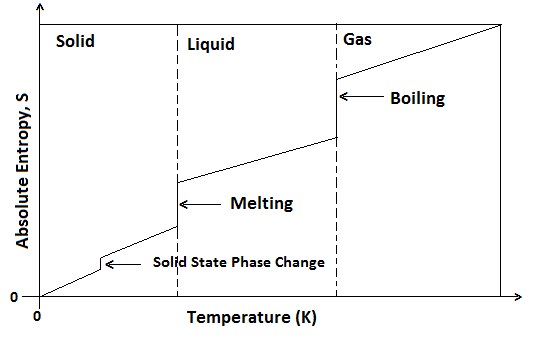
Thus crystalline solids have a minimum disorder of constituent particles and therefore, least entropy while the gases have a maximum disorder of particles and therefore, high entropy. Liquids have entropy in between the solids and gases. Entropy is taken to be zero at absolute zero (0K or -273°C) because at this temperature there is a maximum orderly arrangement of particles in all perfect crystals. With an increase in temperature entropy increases.
The S.I. unit of entropy is joules per kelvin (JK-1).
Characteristics of Entropy:
- Entropy is an extensive property. Its value depends upon the amount of the substance present in the system.
- The entropy of a system is a state function. The change in entropy in going from one state to another is independent of the path. Thus, the change in entropy is given as, ΔS = Sfinal state – Sinitial state.
- The change in entropy for a cyclic process is always zero i.e. ΔS = 0.
- In an irreversible process, ΔSuniverse > 0. This means that there is an increase in entropy of the universe in spontaneous change.
- At absolute zero temperature (0K) entropy of a perfect crystal is taken as zero.
- S.I. unit of entropy is joules per kelvin (JK-1).
- The change in entropy in the equilibrium state is zero (ΔS = 0).
- Larger the space available for a motion of molecules more is the entropy. Example- expansion of gas, evaporation etc.
- An increase in the number of molecules in a chemical reaction also leads to an increase in entropy.
Change in Entropy:
Entropy of a system is a state function. Thus, the change in entropy is given as:
ΔS = Sfinal state – Sinitial state
If ‘q’ is the heat energy evolved or absorbed in a reversible and isothermal process at constant temperature then change in entropy is given by-
ΔS = qrev / T = ΔH / T
Effect of temperature on Entropy:
An increase in temperature increase entropy due to the increase in motion of particles which results in more disorder. At absolute zero, entropy of a perfect crystalline solid is zero. There is increase in entropy as the temperature of a substance rises from absolute zero as disorder of the particle increases.
Entropy and Equilibrium State:
During the spontaneous process, the entropy of the system goes on increasing. When the system reaches the equilibrium state, the entropy of the system becomes maximum and therefore, no more increase in the entropy of the system is possible. Thus, the condition for any system to achieve an equilibrium state is that its entropy becomes maximum. The mathematical condition for entropy (S) to be maximum is that the change in entropy (ΔS) is zero, i.e.
ΔS = 0 (at equilibrium)









Comments (No)