Table of Contents
Buoyancy And Archimedes Principle:
Buoyancy:
You must have noticed that the bodies appear lighter when they are immersed in water or any other liquid. For example- when a cork is immersed underwater and released, it rises and floats on the surface; when a bucket immersed in water is pulled out, it suddenly appears much heavier as soon as it comes above the surface of the water; sailors find difficulty in lifting the heavy anchor of the boat when it is out of water; a stone, difficult to lift on the ground, can be lifted easily when it is underwater. It is a matter of common observation that whenever a body is partly or completely immersed in a liquid, it experiences an upward force or upthrust. This upward force is called the buoyant force or buoyancy.
It acts vertically through the centre of gravity of the displaced liquid, called the centre of buoyancy.
The magnitude of the buoyant force is equal to the weight of the liquid displaced by the immersed body. That is,
Buoyant Force = Weight of the liquid displaced = Vdg
Where ‘V’, ‘d’ and ‘g’ are the volume of the liquid displaced, the density of the liquid and the acceleration due to gravity, respectively.
This fact was first discovered by Archimedes, a Greek mathematician and scientist, who enunciated a principle, known after him as Archimedes’s principle.
Archimedes Principle:
When a body is wholly or partially immersed in a fluid, it suffers a certain loss in its weight which is equal to the weight of the fluid displaced by the body. This is known as the Archimedes principle.
In the above statement, the term fluid means either a liquid or a gas.
Verification of Archimedes Principle:
The Archimedes Principle may be verified by the following experiments-
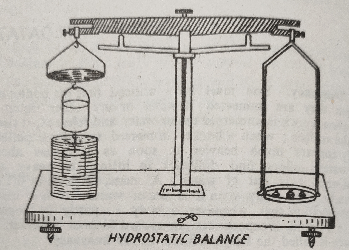
Experiment 1: Take a metallic cylinder and a socket in which the cylinder fits tightly. In such a case, the volume of the cylinder will be equal to the inside volume of the socket. Now take a hydrostatic balance (an ordinary balance with one of its pans much shorter than the other; the shorter pan has on its underside a hook for suspending a solid) and attach a socket to the hook of its shorter pan. Suspend the metallic cylinder from the hook under the socket.
Place weights in the other pan so that the beam becomes horizontal. Now place a beaker containing water under the shorter pan in such a manner that the cylinder completely dips in water but does not touch the bottom or the sides of the beaker. It will be noted that the beam does not remain horizontal when the lever of the balance is raised. In other words, the weights in the other pan will be found to be too heavy. Pour water, carefully, into the socket by means of a pipette and fill it completely. The pans will be found balancing each other only when the socket is completely filled with water. This indicates that the loss of weight experienced by the cylinder is equal to the weight of water filling the socket which is equal to the volume of the cylinder. The loss in weight of the cylinder immersed in water is, thus, equal to the weight of an equal volume of water. The experiment may be repeated by using oil instead of water. In such a case, the loss in weight of the cylinder will be found to be equal to the weight of the oil in the socket.
Experiment 2: Take a spring balance and suspend the socket and the cylinder from its hook in such a manner that the socket is above and the cylinder is below it, as shown in fig. Note the reading of the spring balance. Let its pointer stands at A. Now place a beaker containing water under the spring balance in such a way that the cylinder dips in water completely without touching the side or bottom of the beaker. As the cylinder suffers loss in weight, the pointer will move up, say to a point C. Pour water in the socket. It will be found that the pointer again moves down to A when the socket is completely filled up with water. This indicates that the loss in weight of the cylinder is equal to the weight of water displaced by it.
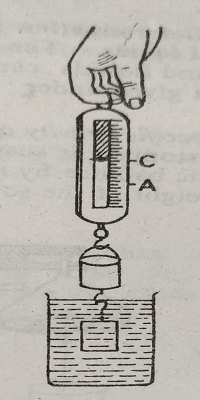









Comments (No)