Exponential Series:
An exponential series is a mathematical expression that represents the sum of an infinite sequence of terms, where each term is a power of a fixed number raised to a non-negative integer power.
You know that the infinite series, Σtn, is said to be convergent when the sum of its first n terms is less than or equal to a finite quantity, however, large n may be. Thus, series, 1 + 1/3 + 1/32 + … to ∞, is convergent which converges to 1/[1 – (1/3)] i.e., to 3/2.
The infinite series, 1 + 1/1! + 1/2! + 1/3! + … to ∞, is convergent and its sum is denoted by the symbol ‘e’.
| Thus, one may write e = 1 + 1/1! + 1/2! + 1/3! + … to ∞ Now, e = 2 + 1/2! + 1/3! + 1/4! + … to ∞ ∴ e > 2 ……….(i) Again, 3! = 3 x 2 x 1 = 6 > 22 ∴ 1/3! < 1/22 4! = 4 x 3 x 2 x 1 = 24 > 23 ∴ 1/4! < 1/23 Similarly, 1/5! < 1/24 , 1/6! < 1/25 and so on. ∴ e = 2 + 1/2! + 1/3! + 1/4! + … to ∞ ……….(ii) < 2 + 1/2 + 1/22 + 1/23 + … to ∞ < 2 + [(1/2) / {1 – (1/2)}] < 3 ……….(iii) From (ii) and (iii), 2 < e < 3 The exact value of e cannot be found out. It is incommensurable (irrational), which can easily be proved by the method of contradiction. If possible, let us suppose that e is rational. Then, one may write e = p/q, where p and q ∈ N (since 2 < e < 3) and q ≠ 1. Then, p/q = 1 + 1/1! + 1/2! + 1/3! + … + 1/q! + 1/(q + 1)! + 1/(q + 2)! + … to ∞ Multiplying both sides by q! we get p (q – 1)! = 2 (q!) + q!/2! + q!/3! + … + 1 + 1/(q + 1) + 1/[(q + 1) (q + 2)] + … = k + f where k = 2 (q!) + q!/2! + q!/3! + … + 1 = a positive integer and f = 1/(q + 1) + 1/[(q + 1) (q + 2)] + … to ∞ < 1/(q + 1) + 1/(q + 1)2 + … to ∞ < [1/(q + 1)] / [1 – 1/(q + 1)] < 1/q But f = 1/(q + 1) + 1/[(q + 1) (q + 2)] + … ⇒ f > 1/(q + 1) ∴ 1/(q + 1) < f < 1/q Thus, f is a positive proper fraction. But p (q – 1)! is a positive integer. Thus, from (iii), it is found that a positive integer = a positive integer + a positive proper fraction, which is absurd. So, e is an incommensurable (irrational) number. The approximate value of e may be taken as 2.7182818 (correct to seven places of decimals). Let n > 1, then 1/n < 1 Using the binomial theorem, we have (1 + 1/n)n = 1 + n (1/n) + [{n (n – 1)}/2!] (1/n)2 + [{n (n – 1) (n – 2)}/3!] (1/n)3 + … = 1 + 1/1! + (1 – 1/n)/2! + [(1 – 1/n) (1 – 2/n)]/3! + …, which is an identity. Now, when n approaches infinity, each of 1/n, 2/n, 3/n, etc., will approach zero. Thus, in the limiting case, when n is very large, (1 + 1/n)n = 1 + 1/1! + 1/2! + 1/3! + … = e |
| Theorem 1: For all real values of x, ex = 1 + x/1! + x2/2! + x3/3! + … to ∞ (exponential series) Proof- Let n > 1, then 1/n < 1. Now, using the binomial theorem, we have, for all real values of x, (1 + 1/n)nx = 1 + nx (1/n) + [nx (nx – 1)/2!] [1/n2] + [nx (nx – 1) (nx – 2)/3!] [1/n3] + … ⇒ [(1 + 1/n)n]x = 1 + x + x (x – 1/n)/2! + x (x – 1/n) (x – 2/n)/3! + … when n → ∞, 1/n → 0, 2/n → 0, 3/n → 0 etc. Thus, in the limiting case, when n is very large, [(1 + 1/n)n]x = 1 + x/1! + x2/2! + x3/3! + … to ∞ ⇒ ex = 1 + x/1! + x2/2! + x3/3! + … to ∞ 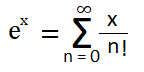 |
| Theorem 2: If a > 0, then ax = 1 + (x/1!) loge a + (x2/2!) (loge a)2 + (x3/3!) (loge a)3 + … to ∞ Solution- From the exponential theorem, we have for all values of z ez = 1 + z/1! + z2/2! + z3/3! + … to ∞ Replacing z by cx, we have ecx = 1 + cx/1! + c2x2/2! + c3x3/3! + … to ∞ ……….(i) Let ec = a, the c loge e = loge a ⇒ c = loge a ∴ ecx = (ec)x = ax Thus, from (i), ax = 1 + (x/1!) loge a + (x2/2!) (loge a)2 + (x3/3!) (loge a)3 + … We have, ex = 1 + x/1! + x2/2! + x3/3! + x4/4! + … Replacing x by -x, e-x = 1 – x/1! + x2/2! – x3/3! + x4/4! – … ∴ (ex + e-x)/2 = 1 + x2/2! + x4/4! + … and (ex – e-x)/2 = x + x3/3! + x5/5! + … Also, e = 1 + 1/1! + 1/2! + 1/3! + 1/4! + … e-1 = 1 – 1/1! + 1/2! – 1/3! + 1/4! – … ∴ (e + e-1)/2 = 1 + 1/2! + 1/4! + … and (e – e-1)/2 = 1/1! + 1/3! + 1/5! + … |
| Example 1: Find the coefficient of x10 in the expansion of e2x. Solution- e2x = 1 + 2x/1! + (2x)2/2! + (2x)3/3! + … ⇒ e2x = 1 + 2x/1! + 22x2/2! + 23x3/3! + … ∴ coefficient of x10 is 210/10! Example 2: Find the coefficient of bn in the series (1 + b)/1! + (1 + b)2/2! + (1 + b)3/3! + … to ∞ Solution- The given series is, (1 + b)/1! + (1 + b)2/2! + (1 + b)3/3! + … = [1 + (1 + b)/1! + (1 + b)2/2! + (1 + b)3/3! + …] – 1 = e1+b – 1 = e1 . eb – 1 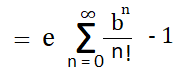 ∴ coefficient of bn is e (1/n!) |
| Example 3: Prove that loge 3 + (loge 3)2/2! + (loge 3)3/3! + … to ∞ = 2 Solution- The given series is- loge 3 + (loge 3)2/2! + (loge 3)3/3! + … to ∞ = (1 + loge 3 + (loge 3)2/2! + …) – 1 = eloge 3 – 1 = 3 -1 = 2 |
| Example 4: Calculate the sum of the series 2/1! + 4/3! + 6/5! + … to ∞ Solution- The given series is, 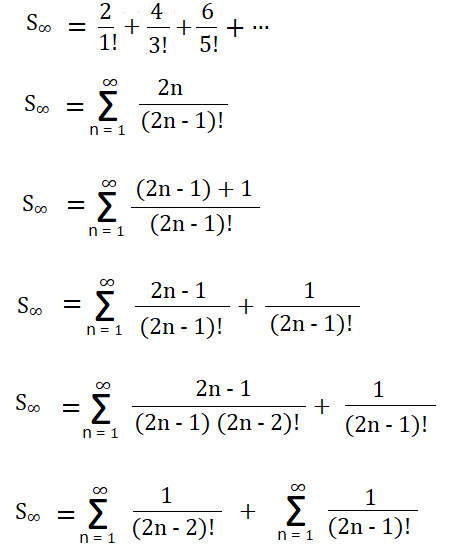 S∞ = (1/0! + 1/2! + 1/4! + …) + (1/1! + 1/3! + 1/5! + …) S∞ = (e1 + e-1)/2 + (e1 – e-1)/2 S∞ = (e + e-1 + e – e-1)/2 S∞ = 2e/2 S∞ = e |









Comments (No)