Trigonometrical Ratios of Multiple Angles:
For any values of A and B, we have-
sin (A + B) = sin A cos B + cos A sin B
cos (A + B) = cos A cos B – sin A sin B
tan (A + B) = (tan A + tan B)/(1 – tan A tan B)
Putting B = A, we get-
sin 2A = 2 sin A cos A ………..(i)
cos 2A = cos2 A – sin2 A …………..(ii)
cos 2A = 2 cos2 A – 1 …………(iii)
cos 2A = 1 – 2 sin2 A …………(iv)
tan 2A = (2 tan A)/(1 – tan2 A) …………(v)
From (iii), we get 2 cos2 A = 1 + cos 2A
⇒ cos2 A = 1/2 ( 1 + cos 2A) ………..(vi)
Also, from (iv) we have-
2 sin2 A = 1 – cos 2A
⇒ sin2 A = 1/2 (1 – cos 2A) ……….(vii)
From (vi) and (vii), one can get-
sin2 A/cos2 A = [1/2 (1 – cos 2A)]/[1/2 ( 1 + cos 2A)] = (1 – cos 2A)/( 1 + cos 2A)
⇒ tan2 A = (1 – cos 2A)/( 1 + cos 2A) ………….(viii)
Also, for any values of A and B, we have-
cot (A + B) = (cot A cot B – 1)/(cot B + cot A)
∴ cot 2A = (cot2 A – 1)/2cot A ………….(ix)
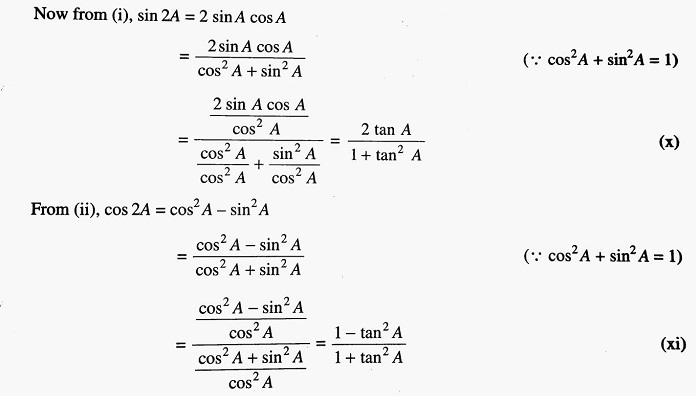
From (x) and (xi), we get the values of sin 2A and cos 2A in terms of tan A. The values cosec 2A and sec 2A can be obtained from the values of sin 2A and cos 2A respectively.
Now, sin 3A = sin (2A + A) = sin 2A cos A + cos 2A sin A = 2 sin A cos A . cos A + (1 – 2 sin2 A). sin A = 2 sin A. cos2 A + sin A – 2 sin3 A = 2 sin A (1 – sin2 A) + sin A – 2 sin3 A = 2 sin A – 2 sin3 A + sin A – 2 sin3 A = 3 sin A – 4 sin3 A ……….(xii)
cos 3A = cos (2A + A) = cos 2A cos A – sin 2A sin A = (2cos2 A – 1) . cos A – 2 sin A cos A . sin A = 2 cos3 A – cos A – 2 sin2 A cos A = 2 cos3 A – cos A – 2 (1 – cos2 A) . cos A = 2 cos3 A – cos A – 2 cos A + 2 cos3A = 4 cos3 A – 3 cos A ……..(xiii)

| Important Formulas: (1) sin 2A = 2 sin A cos A = 2 tan A/(1 + tan2 A) (2) cos 2A = cos2 A – sin2 A = 2 cos2 A – 1 = 1 – 2 sin2 A = (1 – tan2 A)/(1 + tan2 A) (3) tan 2A = 2 tan A/(1 – tan2 A) (4) cot 2A = (cot2 A – 1)/2cot A (5) sin 3A = 3 sin A – 4 sin3 A (6) cos 3A = 4 cos3 A – 3 cos A (7) tan 3A = (3 tan A – tan3 A)/(1 – 3 tan2 A) |








Comments (No)