Table of Contents
Circumcircle and Inscribed Circle of a Triangle:
Circumcircle of a Triangle:
The circle passing through the three vertices of a triangle is called the circumscribing circle or the circumcircle of the triangle. The centre of the circumcircle is called the circumcentre and its radius is known as the circumradius of the triangle. The radius of the circumcircle of a triangle is denoted by R. The circumcentre of a triangle is the point of intersection of the perpendicular bisectors of its sides.
| In △ABC with BC = a, CA = b and AB = c, a/sin A = b/sin B = c/ sin C = 2R, where R is the circumradius of the triangle |
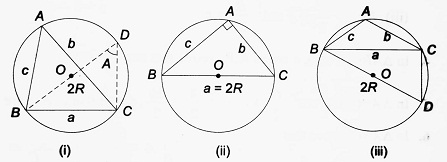
Proof: The centre of the circumcircle is denoted by O. We consider the three possibilities regarding the angle A of △ABC.
| Case (i) When A < 90°. BO is produced to meet the circle at D [Fig (i)] ∴ ∠BDC = ∠BAC = A (angle in the same segment) ∠BCD = 90° (angle in the semicircle) ∴ sin A = sin ∠BDC = BC/BD = a/2R ⇒ a/sin A = 2R |
| Case (ii) When A = 90°. In this case, the hypotenuse BC passes through the centre of the circumcircle and is equal to 2R [Fig (ii)] Here, a/sin A = BC/sin 90° = 2R/1 = 2R |
| Case (iii) When A > 90°, BO is produced to meet the circle at D. In this case ABDC is a cyclic quadrilateral [Fig (iii)] ∴ ∠BAC + ∠BDC = 180° ∴ ∠BDC = 180° – A ∴ ∠BCD = 90° ∴ BC/BD = sin ∠BDC = sin (180° – A) ∴ a/2R = sin A ⇒ a/sin A = 2R |
| Similarly, considering the angles B and C also one can prove that b/2R = sin B and c/2R = sin C Thus, a/sin A = b/sin B = c/sin C = 2R This is sometimes referred to as the R-sine formula. |
| Corollary: We have, a/sin A = 2R ∴ sin A = a/2R Now, area of △ABC is given by △ = (1/2) bc sin A = (1/2) bc . a/2R = abc/4R ∴ R = abc/4△ |
Inscribed Circle or Incircle of a Triangle:
A circle touching all the three sides of a triangle internally is called the incircle of a triangle. The centre of the circle is known as the incentre and the radius of the circle is called the inradius of the triangle. The inradius of a triangle is denoted by r. The incentre of a triangle is the point of intersection of the internal bisectors of its angles.

In △ABC, I is the incentre. D, E and F are points of contact of the sides BC, CA and AB respectively with the circle.
Then, ID = IE = IF =r, the inradius of the Circle.
| Clearly, △ = area of △ABC ⇒ △ = area (△IBC) + area (△ICA) + area (△IAB) ⇒ △ = (1/2) BC x ID + (1/2) CA x IE + (1/2) AB x IF ⇒ △ = (1/2) ar + (1/2) br + (1/2) cr ⇒ △ = (1/2) r (a + b + c) = (1/2) r . 2s = rs ∴ r = △/s |










Comments (No)