Table of Contents
Vapour Pressure and Raoult’s Law:
Raoult studies the vapour pressure of a number of binary solutions and put forward a generalization known as Raoult’s law.
Raoult’s Law for Binary Solution of Volatile Liquids:
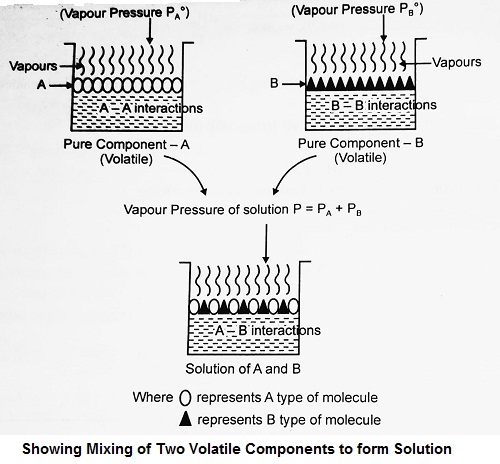
In the binary solutions of volatile liquids, the vapour phase consists of vapours of both components. Raoult’s law for such binary solutions may be defined as:
“At a given temperature, for a solution of volatile liquids, the partial vapour pressure of each component is equal to the product of the vapour pressure of the pure component and its mole fraction”.
Suppose a binary solution consists of two volatile liquids A and B. If PA and PB are the partial vapour pressures of the two liquids and xA and xB are their mole fractions in solution, then
| PA = PA° xA PB = PB° xB |
Where PA° and PB° are the vapour pressure of the two pure liquid components A and B respectively.
Raoult’s Law for Solutions Containing Non-Volatile Solutes:
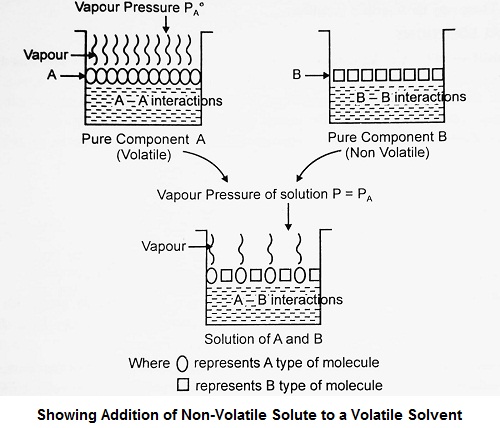
For a solution containing a non-volatile solute, there is no contribution of the solute to the total vapour pressure of the solution. Therefore, the vapour pressure of the solution will be the vapour pressure due to solvent only.
Vapour pressure of the solution = Vapour pressure of the solvent in the solution
If PA is the vapour pressure of the solvent over a solution containing non-volatile solute and xA is its mole fraction, then according to Raoult’s law,
| PA = PA° xA or P(solution) = PA° xA (∵ P = PA) i.e., P (solution) = P (pure solvent) x mole fraction of solvent |
Thus, for solutions containing non-volatile solutes, Raoult’s law may be stated as “At a given temperature, the vapour pressure of a solution containing non-volatile solute is directly proportional to the mole fraction of the solvent”.









Comments (No)