Table of Contents
Work And Power:
Work:
In everyday conversation, we often use the term ‘Work’ to mean any labor which requires either physical or mental effort. Thus, the term work gives us an idea of something being done. For instance, a student solving a numerical problem of mathematics is engaged in a mental activity whereas a gate-keeper standing outside gate of a cinema hall is engaged in a physical activity. Hence, both of them are said to be doing work. However, in the language of physics, the term work has a special meaning. A mechanical work is done when a body starts moving under the influence of a force.
“Work is said to be done by a force when the force produces a displacement in the body on which it acts in a direction not perpendicular to the direction of the force.“
A force does no work if it does not produce displacement in the body on which it acts. Whenever a force acts upon a body in such a manner that the motion of the body takes place the work is said to be done by the force. For instance, an engine in pulling a train does work against the force of friction, and a laborer lifting a load does work against the force of gravity. In physics, work means accomplishment and not fatigue. For instance, a man does no work if he merely supports an attache-case on his head for some time though he may be experiencing muscular fatigue. Similarly, a person may try to move a big stone, in the language of physics, he has done no work if he does not succeed in moving this big stone even though he may have perspired from top to toe. Hence the conditions for work to be done are as under:
- Some force must act upon the body.
- The body must move in the direction of the force.
Evidently, the work done by a force acting on a body is equal to the force multiplied by the distance through which the body moves in the direction of the applied force. In other words, the amount of work done (W) by a force on a body is measured by the product of the applied force (F) and the distance (S) through which the point of application of force moves in the direction of the force.
Mathematically, we have-
Work = Force X Distance or W = F x S ………….(1)
Where ‘W’ is the work done, ‘F’ is the force acting upon the body and ‘S’ is the distance moved in the direction of the applied force.
It is evident from the relation (1) that if there is no displacement, no work is done.

In case, the body moves in a direction making an angle θ with the line along which the force ‘F’ acts, the force can be resolved into two components namely F cos θ along OB and F sin θ along OC. Of these, it is only the component F cos θ of the force in the direction of motion which produces a displacement in the body. The component F sin θ of the force perpendicular to the direction of motion does not work as no displacement of the body takes place in the direction OC. The work done by a force depends upon the magnitude of the force and the displacement produced. The work done by a force on a body is the product of the component of the force in the direction of motion and the distance moved. This relation is expressed mathematically as:
W = F cos θ X S ………………(2)
The reaction (2) is applicable to all general cases, where ‘θ’ is the angle between the displacement ‘S’ and the applied force ‘F’. It is evident from this relation that:
(a) If a force acting on a body is unable to move the body, then force does no work. In this case, S = 0.
Therefore, W = F cos θ X S = F cos θ X 0 = Zero
(b) If a body moves in a direction perpendicular to that in which the force acts, then force does no work. In this case, θ = 90°, cos 90 = 0.
Therefore, W = F cos θ X S = F cos 90 X S = 0 X S = Zero
(c) If a body moves in the direction of the force, the work done is measured by the product of the applied force and the distance moved. In this case, θ = 0, cos 0 = 1.
Therefore, W = F cos θ X S = W = F cos 0 X S = F X S
Consider the case of a body of mass ‘m’ falling vertically through a height ‘h’ under the influence of force of gravity. The body moves in the direction of force (mg) of gravity. The work done ‘W’ by the force ‘mg’ of gravity is expressed as-
W = F X S = mg X h = mgh
Work is a scalar quantity (having only a magnitude but no direction) though both the quantities namely force and displacement involved in its definition are vector quantities (having both a magnitude as well as direction).
Kinds of Work:
Work is of two types namely- Positive Work and Negative Work.
Positive Work:
As we know, work is essentially a scalar quantity. Work is considered to be positive when the force or its component parallel to the line of motion acts in the direction of the displacement. For instance, if a car is accelerated from a stop to some velocity, we conclude that the work is done on the car and this work increases the kinetic energy of the car. This is referred to as positive work. Positive work is work which increases the kinetic energy of the body.
Negative Work:
Work is considered to be negative when the force or its component parallel to the line of motion acts in a direction opposite to that of the displacement. For instance, if an object is moving and we apply a force in such a way as to slow it down the kinetic energy of the object decreases and the work is said to be negative work. Thus, negative work is work which decreases the kinetic energy of the body.
Work is always done by a force against some resistance which opposes motion. Usually, the work done on a body is considered to be negative and the work done by a body is considered to be positive. A typical instance of this phenomenon is a time-piece. In this case, the work is done in winding a spring of the time-piece and this work is referred to as negative work. The spring of the time-piece in turn does work in operating the inside mechanism and this work by the time-piece is referred to as positive work.
Units of Work:
As discussed earlier, the work is measured by the product of the force and the distance moved in the direction of force. Evidently, the unit of work will depend on the units of force and distance.
The unit of work is the amount of work done when a unit force moves a body through a unit distance in the direction of the force.
In C.G.S system, the absolute unit of work is known as erg. It is the amount of work done by a force of one dyne in moving a body through a distance of one centimetre in the direction of force.
1 erg = 1 dyne X 1 cm
In M.K.S or S.I. system, the unit of work is called a Joule or newton metre. It is the amount of work done by a force of one newton in moving a body through a distance of 1 metre in the direction of the force.
1 Joule = 1 newton X 1 metre = 105 dynes X 100 cm = 107 dynes X cm = 107 ergs
Thus, the S.I. unit of work Joule (J) is 107 times the unit of work erg in the C.G.S. unit.
Power:
In physics, the term power means the rate of doing work. It is measured by the amount of work done in a unit time.
Mathematically, we can express power as-
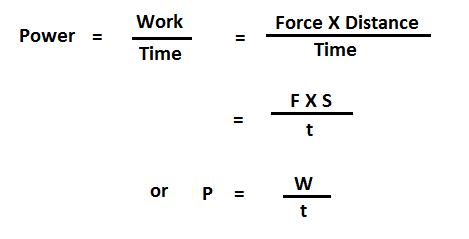
Where ‘P’ is the power, ‘W’ is the work done and ‘t’ is the time taken.
From the above relation it is evident that smaller is the time ‘t’ in which a body can do a given amount of work ‘W’, greater is the power ‘P’ of the body.
Units of Power:
Like work, power is also a scalar quantity. A unit power is the power of an agent which does unit work in unit time.
In the C.G.S system, the absolute unit of power is 1 erg per second. In the M.K.S. system, the absolute unit of power is 1 Joule per second.
The practical unit of power or S.I unit of power in the C.G.S system is referred to as watt. A watt is defined as the power of an agent that works at the rate of one Joule per second. In other words, it is the power of doing 107 ergs of work per second.
1 watt = 107 erg of work per second = 1 Joule per second
The bigger units of power are called a kilowatt and a megawatt.
1 kilowatt = 1000 watts
1 megawatt = 106 watts
Evidently, one kilowatt is the power of an agent that works at the rate of 1000 Joules per second or 1010 ergs per second. Another unit of power in the F.P.S. system is called horsepower (hp).
Thus, one horsepower is the power of an agent which works at the rate of 550 ft. pounds per second.
1 hp = 746 watts = 0.746 kilowatt









Comments (No)