Basic Proportionality Theorem (Thales Theorem)

Basic Proportionality Theorem:

Theorem 1: In a triangle a line drawn parallel to one side, to intersect the other two sides then it divides the two sides in the same ratio.

Given: A △ABC in which DE || BC and intersects AB and AC in D and E respectively.

To prove: AD/DB = AE/EC

Construction: Join BE and CD. Draw EF ⊥ AB and DG ⊥ AC.

Proof: In the figure, Area (△ADE) = (1/2) AD . EF

(Here AD is considered as the base of △ADE and EF is the altitude).

Area (△BDE) = (1/2) DB . EF

(Here DB is the base of △BDE and EF is the altitude).

∴ Area (△ADE)/Area (△BDE) = [(1/2) AD . EF]/[(1/2) DB . EF] = AD/DB ……….(i)

Again, we write area (△ADE) = (1/2) AE . DG

(Here AE is considered as base and DG as the altitude of △ADE)

Also, area (△CDE) = (1/2) EC . DG

(Here EC is considered as base of △CDE and DG is the altitude)

∴ Area (△ADE)/Area (△CDE) = [(1/2) AE . DG]/[ (1/2) EC . DG] = AE/EC ……….(ii)

Since △BDE and △CDE are on the same base DE and between the same parallel lines DE and BC,

∴ area (△BDE) = area (△CDE) ……….(iii)

From (i), (ii) and (iii) it follows that AD/DB = AE/EC

Hence, the theorem is proved.

Theorem 2: (Converse of Basic Proportionality theorem). If a line divides any two sides of a triangle in the same ratio, then the line must be parallel to the third side.

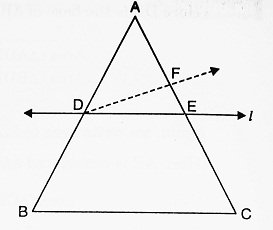
Given: A △ABC and a line ‘l‘ intersecting AB in D and AC in E such that AD/DB = AE/EC.

To prove: l || BC.

Proof: If possible, we suppose that the line ‘l‘ is not parallel to BC. Therefore, there is some other line through D, which is parallel to BC. Let this line be DF. Since DF || BC, therefore, by Thales theorem, we get

AD/DB = AF/FC ………(i)

and AD/DB = AE/EC (given) ………(ii)

∴ (i) and (ii) imply that

AF/FC = AE/EC

⇒ 1 + AF/FC = 1 + AE/EC [∵ Adding 1 to both sides]

⇒ (FC + AF)/FC = (EC + AE)/EC

⇒ AC/FC = AC/EC ………(iii)

∵ (iii) is possible only if the points F and E coincides.

∴ DF is the line ‘l‘ itself. Hence l || BC.