Table of Contents
Depression in Freezing Point:
It is the temperature when the solid and the liquid forms of the substance are in equilibrium with each other, i.e., the solid and the liquid form of the substance have the same vapour pressure and co-exist with each other. It is characteristic of each liquid. For Example- the freezing point of H2O is 273.15 K.
It is observed that the vapour pressure of the solution is lower than the pure solvent. Thus a solution has to be cooled further to get the freezing point of the solution. The decrease in the freezing point of the solution due to the addition of non-volatile solute to solvent is called depression in freezing point. It is denoted by ΔTf.
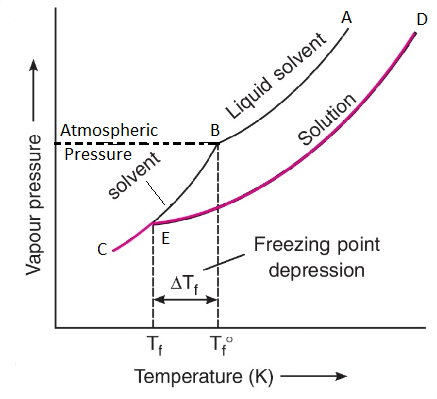
This depression in freezing point can also be explained by plotting vapour pressure versus temperature curve as shown above in the figure. T1 is the freezing point of the solvent and T2 is the freezing point of the solution (T2 < T1). Therefore, ΔTf = (T2 – T1).
Expression for Depression in Freezing Point:
| We know that, ΔTf ∝ ΔP ……….(i) Again by Raoult’s law, ΔP ∝ xB ……….(ii) Therefore, ΔTf = k . xB [Where xB is the mole fraction of solute in solution] ⇒ ΔTf = (k . nB) / (nA + nB) = k (nB/nA) [Since solution is dilute and nB << nA] ⇒ ΔTf = k . nB / (WA/MA) = k . MAnB / WA = kf (nB/WA) ……….(iii) [Where MA is molecular mass of solvent and WA = weight of solvent] Where kf is a new constant (kf = k . MA) called molal depression constant or cryoscopic constant. If the weight of solvent (WA) is 1 kg, then nB/WA = molality (m) Therefore, ΔTf = kf . m ……….(iv) If m = 1; ΔTf = kf. Thus, molal depression constant is the depression in freezing point when molality of a solution is unity. Its unit is K/m or K kg mol-1. Its value for H2O is 1.86 K kg mol-1 at 273 K. |
Calculation of Molecular Mass of Solute from ΔTf:
| From (iv), we have ΔTf = kf . m = kf (nB / WA) X 1000 [Since molality is in terms of 1000 gm] Therefore, ΔTf = (kf . WB . 1000) / (MB . WA) ⇒ MB = (kf . WB . 1000) / (ΔTf . WA) Hence, molecular mass of solute (MB) is calculated. |









Comments (No)