Fraunhofer Diffraction at a Single Slit:

(I) Let a parallel beam of monochromatic light of wavelength ‘λ’ be incident on a slit of width ‘d’ as shown in the figure.
(II) According to Huygen’s theory, every point of the wavefront in the plane of the slit acts as a secondary source and sends secondary waves in all directions.
(III) The rays travelling normally are made to focus at ‘P’ and rays diffracted through ‘θ’ are made to focus at P’. Thus in figure AB, CD and EF are diffracted rays through angle ‘θ’.
(IV) To find out the resultant intensity at point ‘P’ draw AG perpendicular to all diffracted rays.
Thus, the path difference between extreme diffracted rays is-
| Path Difference = EG = d sin θ ……….(i) and Phase Difference = (2π/λ) d sin θ ……….(ii) |
(V) Let us consider that the given slit is divided into ‘N’ number of very small parallel slits and ‘a’ be the amplitude of wave from each slit.
∴ The phase difference between any two successive waves will be-
| (Total phase) x 1/N = 1/N [(2π/λ) d sin θ] ……….(iii) |
(VI) Since the secondary waves from each point of the slit are oriented from the same incident wavefront, their amplitudes are the same, hence the intensity distribution at point ‘P’ is due to phase difference only. The condition for the resultant can be derived by using the amplitude phase diagram as shown in figure (2).
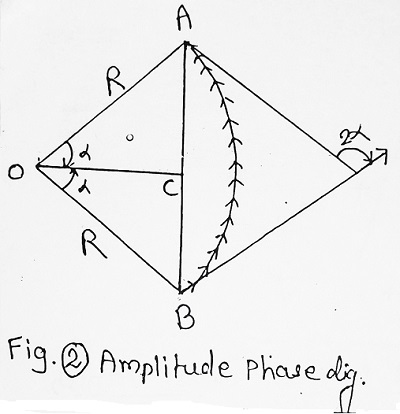
| Consider that the slit is divided into a large number of strips, say ‘N’ due to which the phase diagram takes the form of an arc of a circle of a radius R, say. The distribution of intensity at point P due to each strip changes from 0 to [(2π/λ) d sin θ] (i.e. 0 to 2α). Now the resultant amplitude is AB = A, say. From right-angled △OCB, sin α = BC/R ⇒ BC = R sin α But resultant amplitude A = AB = 2CB ⇒ A = 2R sin α ……….(iv) Now the total number of slits is ‘n’, each having amplitude ‘a’ and ‘2α’ is the phase angle between 1st and last amplitude vector (i.e. secondary wavelet). ∴ 2α = Arc/radius = Na/R ⇒ R = Na/2α ……….(v) Using (v) in (iv), we get- Resultant Amplitude = 2R sinα = Na. sin α/α i.e. A = Na. sin α/α = A0 sin α/α ……….(vi) Where A0 = Na = total or maximum amplitude of disturbance due to ‘N’ wavelets each of amplitude ‘a’. ∴ Resultant Intensity is I ∝ A2 or I ∝ A02 (sin α/α)2 ……….(vii) |
Conditions of Maxima and Minima:
| Case I- Principal Maximum: We have, A = A0 sin α/α For A to be maximum i.e. for A = A0, sin α/α should be ‘1’. ⇒ A = (A0/α) sin α ⇒ A = (A0/α) [α – α3/3! + α5/5! – α7/7! + ———-] ⇒ A = A0 [1 – α2/3! + α4/5! – α6/7! + ———-] Thus for ‘A’ to be maximum, negative terms must vanish. ⇒ α = 0 i.e. (2π/λ) d sin θ = 0 ⇒ θ = 0 ……….(viii) i.e. principal maximum is produced at θ = 0, due to secondary wavelets which travel normally to the slit (in fig at point P, there will occur maximum intensity). |
| Case II- Condition for Minima: We have, A = A0 sin α/α For A to be minimum, sin α = 0, thus all values of α satisfying the conditions except central maximum gives minima. ⇒ α = ± nπ, n ≠ 0, but n = 1, 2, 3, …….. ⇒ α = (π/λ) d sin θ = ± nπ ⇒ d sin θ = ± nλ ……….(ix) This gives the points of minimum intensity on both sides of the principal maximum. |
| Case III- Secondary Maxima: The condition for secondary maxima is path difference should be equal to (2n + 1) λ/2. Path Difference = (2n + 1) λ/2 and Phase Difference = (2π/λ) x path difference ⇒ Phase Difference = (2π/λ) x (2n + 1) λ/2 = (2n + 1) π, n ≠ 0, n = 1, 2, 3, ……. |









Comments (No)