Table of Contents
Kirchhoff’s Laws:
There are two laws as follows-
Kirchhoff’s 1st Law or Kirchhoff’s Junction Law:
Statement- It states that the algebraic sum of currents meeting at a junction in a closed circuit is zero. This law is also known as Kirchhoff’s current law. Kirchhoff’s 1st law supports the law of conservation of charge i.e. Σ I = 0.
Sign Convention- The currents flowing in a conductor towards the junction are taken as positive and the currents flowing away from the junction are taken as negative.

Example- Consider a junction ‘O’ in the electrical circuit at which the five conductors are meeting.
Let I1, I2, I3, I4 and I5 be the currents in these conductors in directions as shown. Then according to Kirchhoff’s 1st law,
| -I1 – I2 + I3 – I4 + I5 = 0 ⇒ Σ I = 0 |
Kirchhoff’s 2nd Law or Kirchhoff’s Loop Law:
Statement- It states that in a closed-loop, the algebraic sum of e.m.f.’s is equal to the algebraic sum of the product of resistances and the respective currents flowing through them. Basically, Kirchoff’s 2nd law supports the law of conservation of energy i.e.
| Σ E = Σ IR |
Sign Convention-
- While traversing in a loop, if the negative pole of the battery comes first, then e.m.f. is taken as positive and vice versa.
- While traversing in a loop, if we are moving in the same direction of current, then the product of resistance and the current in that resistance is taken as positive and vice versa.
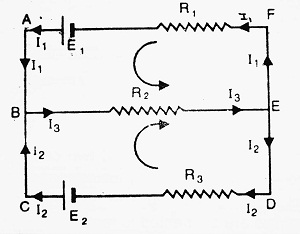
Example- Consider a closed circuit as shown in the figure, containing two cells of e.m.f. E1 and E2 and three resistors R1, R2 and R3. Let I1, I2, I3 be the currents through R1, R2, R3 respectively.
Apply Kirchhoff’s loop law to loop ABEFA,
| +E1 = +I3R2 + I1R1 |
Apply Kirchhoff’s loop law to loop ABCDEFA,
| -E2 + E1 = -I2R3 + I1R1 ⇒ Σ E = Σ IR |









Comments (No)