Rolle's Theorem | Important Concept

Rolle’s Theorem:

Michael Rolle (1652-1719), a French mathematician gave this useful theorem on calculus which is very helpful in estimating the extrema of various functions in given intervals.

Theorem: If f(x) is a real-valued function such that

f(x) is continuous on the closed interval [a, b], i.e., on a ≤ x ≤ b
f'(x) exists on the open interval (a, b), i.e. on a < x < b.
f(a) = f(b), then there exists at least one value c of x in the open interval a < x < b such that f'(c) = 0.

f'(c) = 0 means slope of the tangent to the curve y = f(x) at x = c is zero i.e., the tangent to the curve y = f(x) is parallel to the X-axis.

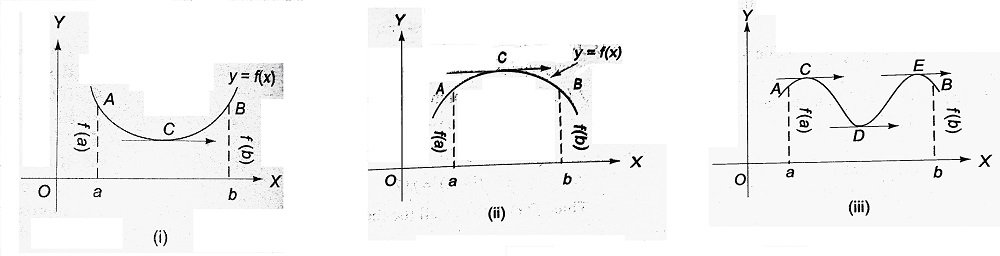
Geometrical Interpretation- Since f(x) is a continuous function on [a, b], the graph of the function is a continuous curve from point A where x = a to point B where x = b.

Again as f(x) is differentiable on the interval (a, b), the graph of f(x) has a unique tangent at any point between A and B.

f(a) = f(b) implies that values of the function at x = a and x = b are equal.

The theorem states that if a function f(x) satisfies the above three conditions namely continuity in the closed interval a ≤ x ≤ b, differentiability in the open interval a < x < b, and equality of the functional values at the extreme points x = a and x = b, then, there must be at least one point x = c in the open interval where the tangent drawn to the curve is parallel to the X-axis.

Note: Rolle’s theorem is applicable to a function that satisfies all the three conditions stated above. To check the applicability of Rolle’s theorem to a function, the following points are very helpful.

Polynomial functions are continuous everywhere on R.
sin x, cos x, and e^x are continuous for all x ∈ R.
log x is continuous for all x > 0.
tan x and sec x are discontinuous at x = (2n + 1) π/2, where n ∈ Z.
cosec x and cot x are discontinuous at x = nπ, where n ∈ Z.
| x | is not differentiable at x = 0.
| x | is not continuous at x = n, where n ∈ Z.
If f(x) and g(x) are continuous and differentiable functions on [a, b], then the functions f(x) ± g(x), f(x)g(x) are also continuous and differentiable on [a, b]. The function f(x)/g(x) is also continuous and differentiable in the said interval, provided g(x) ≠ 0.
If f(x) is derivable everywhere on [a, b], then it must be continuous there.
f(x) = √(x – α) is continuous in the interval x ≥ α and φ(x) = √(α – x) is continuous in the interval x ≤ α.