Lami's Theorem | Important Concept

Lami’s Theorem:

If three forces acting on a particle keep it in equilibrium, then each is proportional to the sine of the angle between the other two.

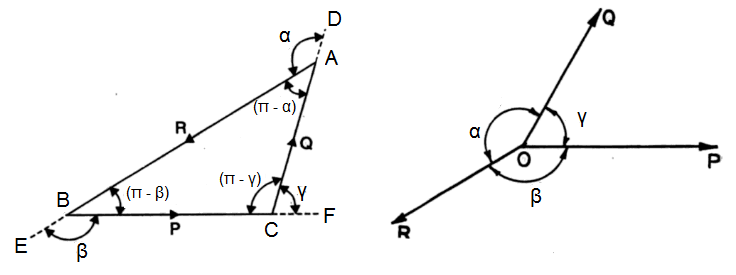
Proof- Let the three forces P, Q_, and R acting on a particle O be in equilibrium and let α, β, and γ be the angles between Q and R, R and P, P and Q respectively.

Since the forces P, Q, and R acting at point O are in equilibrium, they can be represented by the sides BC, CA, and AB of △ABC, drawn parallel to the directions of P, Q, and R respectively.

∴ ∠BAD = α, ∠CBE = β, and ∠ACF = γ
∴ ∠BAC = π – α, ∠ABC = π – β, and ∠ACB = π – γ

Now, P, Q, and R are represented by BC, CA, and AB respectively.

∴ P/BC = Q/CA = R/AB ……….(i)

From sine rule, we have
BC/sin ∠BAC = CA/sin ∠ABC = AB/sin ∠ACB
⇒ BC/sin (π – α) = CA/sin (π – β) = AB/sin (π – γ)
⇒ BC/sin α = CA/sin β = AB/sin γ ……….(ii)

From (i) and (ii) we get
P/sin α = Q/sin β = R/sin γ