Table of Contents
Coordination Number, Void, Ionic Radii, and Radius Ratio Rule:
Coordination Number:
It is the number of spheres that are in contact with a particular sphere in the closest packing. Both hexagonal close packing (hcp) and cubic close packing (ccp) modes of stackings have a coordination number of 12 because a sphere in these arrangements has 12 closest neighbours- 6 other spheres in its own layer, 3 spheres in the layer above and 3 in the layer below.
Factors affecting coordination number:
- Size of central particle- If the central particle is small in size then it can accommodate a lesser number of peripheral particles compare to a situation where the central particle is large in size.
- Size of peripheral particles- If the size of peripheral particles is smaller then the coordination number of the central particle will be larger compare to a situation where particles size of peripheral particles is larger.
- Temperature and pressure- Increase in pressure decreases the interparticle distance hence increases coordination number and reverse happen if the temperature is low.
Type of Voids:
In hcp as well as in ccp, only 74% of the available space is occupied by spheres. The remaining space (26%) left unoccupied between the spheres in close packing constitutes interstices, voids or holes. On arranging the 2nd layer of spheres over triangular voids (B or C) of the first layer, two types of voids are obtained in three-dimensional close packing.
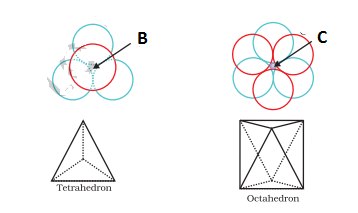
- Tetrahedral Voids- These are ordinary voids in the 2nd layer over the spheres of the first layer and are shown in the figure as ‘B‘ voids. Thus a simple triangular void bounded by four spheres (one of the first and three of the 2nd) is known as a Tetrahedral void because the centres of these four spheres are at the corners of a regular tetrahedron. In close packing, the number of tetrahedral voids is double the number of spheres; one above the sphere and one below the sphere. The radius of the tetrahedral void relative to the radius of the sphere is 0.225 i.e. rvoid = 0.225 x rsphere.
- Octahedral Voids- These type of voids are produced by the combination of two triangular voids, one of the second layer and the other unoccupied void of the first layer and are shown in the figure as ‘C‘ voids. Thus a double triangular void bounded by six spheres is known as an octahedral void because this is enclosed between six spheres, the centres of which occupy corners of a regular octahedron. The number of octahedral voids is equal to the number of spheres. The radius of the octahedral void relative to the radius of the sphere is 0.414 i.e. rvoid / rsphere = o.414. Thus, an octahedral void is larger than a tetrahedral void.
Ionic Radii:
If ions are considered to be spheres, then the radius of the sphere is ionic radii or it may be defined as the distance from the centre of the nucleus up to the point the electron cloud of that ion exists. It shows an increasing trend on moving down a group from top to bottom while a decreasing trend on moving from left to right along a period.
Radius Ratio Rules:
In crystals generally, the anions (larger ions) form a close-packed arrangement and the cations (smaller ions) fit into the interstitial sites. For the stability of an ionic compound, each cation should be surrounded by a maximum number of anions and vice-versa which depends upon the radius ratio. Radius Ratio may be defined as the ratio of the radius of cation to the radius of the anion of the ionic solid.
Radius Ratio = Radius of the Cation (r+)/Radius of the Anion (r–)
A cation will fit exactly into an octahedral void and would have a coordination number of six if r+/r– = 0.414.
Similarly, if r+/r– = 0.225, the cation will fit exactly into a tetrahedral void and have a coordination number of four. The relationship between the radius ratio, coordination number and the structural arrangement is called radius ratio rules and are given below-
| Radius Ratio (r+/r–) | Coordination Number of Cation | Structural Arrangement of Anions around the Cation | Examples |
|---|---|---|---|
| 0 to 0.155 | 2 | Linear | —– |
| 0.155 – 0.225 | 3 | Plane-Triangular | B2O3 |
| 0.225 – 0.414 | 4 | Tetrahedral | ZnS |
| 0.414 – 0.732 | 6 | Octahedral | NaCl |
| 0.732 – 1.000 | 8 | Body-Centred Cubic | CsCl |
- Differences Between Spermatogenesis And Oogenesis
- Passive and Active Absorption of Food
- Alimentary Canal of Man
- Differences Between Algae And Fungi
- Essential and Non-essential Parts of the Flowers
- Pollination: Types and Its Importance
- Enzymes And Their Properties
- Constituents of Food: Carbohydrates, Proteins, Fats & Vitamins
- Nutrition and Digestion-NIOS









Comments (No)