Table of Contents
Close Packing in Two and Three Dimensions:
The structure of a solid is the result of close packing of its constituent particles and the type of packing in which the available space is used most economically is regarded as a stable one. For representing the packing of constituent particles in solids, the constituent particles are represented as spheres of equal size.
The placement of a number of such spheres side by side in a horizontal row so that their centres lie along a straight line is known as “Edge of Crystal“.
The combination of a number of such rows lying side by side and touching each other is known as “Crystal Plane“.

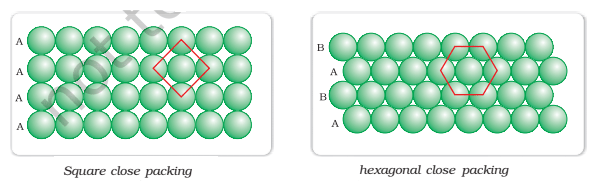
Close packing in Two Dimensions:
These rows of spheres can combine in two ways having two dimensional packing as follows-
- When the spheres are arranged in such a way that the spheres in the adjacent rows lie just one over the other and show a horizontal as well as vertical alignment and form squares, then this type of packing is called square close packing. In this combination, each particular sphere is contact with four neighbouring spheres.
- When the rows of spheres are arranged in such a way that the spheres in every second row are placed in the depression between the spheres of the first row such that the spheres in the 3rd row are vertically aligned with the spheres of the first row and so on. In such a combination, each particular sphere is in contact with six neighbouring spheres which are arranged hexagonally around it and is known as hexagonal close packing. The hexagonal close packing is more efficient than square close packing because in hexagonal close packing 60.4% of the available space is occupied by spheres whereas in square close packing only 52.4% of the space is occupied by spheres.
Close packing in Three Dimensions:
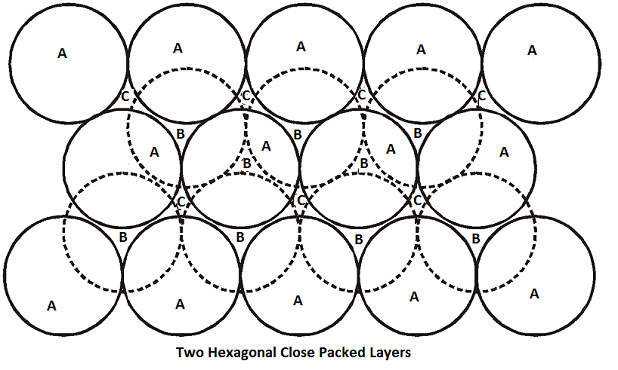
The real structure of a solid is the result of three-dimensional packing of spheres which is obtained by placing layers of closed packed spheres one above the other and retaining hexagonal close packing in the first layer because it is more efficient. For close packing, each sphere in the 2nd layer is placed in the holes or voids at the centre of three touching spheres of the first layer. The spheres in the first layer are shown by solid lines (marked as A) and the two types of voids between the spheres are marked as ‘B’ and ‘C’ while the spheres in the 2nd layer are shown by broken lines. The 2nd layer of spheres may be placed either on the holes marked ‘B’ or on holes marked ‘C’ i.e. only half the triangular voids in the first layer are occupied by spheres in the 2nd layer. The unoccupied holes or voids in the first layer are shown by ‘C’ in the figure. The third layer of spheres is placed over the second layer in two different ways-
- The 3rd layer of spheres may be placed on ‘B’ voids of the 2nd layer so that each sphere of the 3rd layer lies directly over a sphere of the first layer giving rise to a three dimensional closest packing in which the spheres in every alternate layer are vertically aligned. This type of arrangement called AB AB……. arrangement has hexagonal symmetry and is known as Hexagonal close packing (hcp). Example- Mg, Be and Zn have hcp arrangement.
- The 3rd layer of spheres may be placed over ‘C’ voids in the 2nd layer giving rise to a type of 3-dimensional closest packing in which the spheres in every 4th layer are vertically aligned. This type of arrangement called ABC ABC………. arrangement has cubic symmetry and is known as Cubic close packing (ccp) having an fcc unit cell. Example- Fe, Cu, Ag, Au, Al, Ni etc. have ccp arrangement.
Both the above patterns of stacking spheres though different in form are equally efficient. They occupy the maximum possible space which is about 74% of the available volume, hence they are called closed packed structures.









Comments (No)