Table of Contents
Shapes of Atomic Orbitals:
s- Orbitals:
When a graph is plotted between the probability of finding the electron (ψ2) and its difference from the centre of the nucleus, the curve thus obtained is known as “Probability Distribution Curve“. The probability distribution curve for 1s orbital shows that the probability of finding the electron is maximum near the nucleus and goes on decreasing as the distance from the nucleus increases. But the curve never touches the abcissa indicating that there is always some probability of finding the electron even at a large distance from the nucleus. The probability distribution curve for 2s orbital shows that the probability is maximum near the nucleus and decreases to zero with distance and again increases and then decreases till it becomes almost zero at large distances. The shape of s orbital may be predicted by two ways-
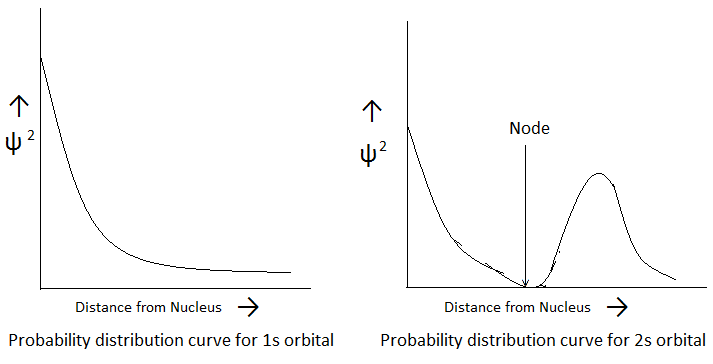
- On the basis of Probabilities- The probability of finding the electron in s orbital of any shell is found to be equal in all directions at a given distance from the nucleus. Hence, s orbitals are non-directional and spherically symmetrical about the nucleus, since a sphere can be defined completely by a single value.
- On the basis of Quantum Numbers- For s orbital, l = 0 and m = 0, (l = Azimuthal Quantum Number and m = Magnetic Quantum Number). Thus, s orbital has only one orientation. The only three-dimensional figure having one orientation in space is a sphere, hence, s orbital is spherical in shape. The size of s orbital depends upon Principal Quantum Number (n). Graeter the value of ‘n’, larger is the size of orbital. Therefore, 2s orbital is larger in size than 1s orbital. In 2s orbital, there is a spherical shell where the probability of finding the electron is almost zero. This spherical shell is called a ‘Node’ or ‘Nodal Surface’. This 2s orbital differs from 1s orbital in having a nodal sphere within it. The total number of spherical nodal surfaces within s orbital of any shell (n) is equal to (n-1).
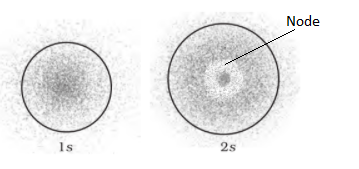
p-Orbitals:
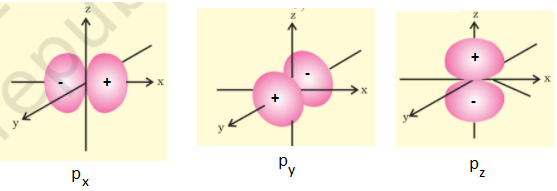
On the basis of probability calculations, it is found that the probability of finding the p-electrons is maximum in two lobes on the opposite sides of the nucleus indicating that p-orbital is “dumb-bell” in shape. The probability of finding a particular p-electron is equal in both the lobes. There is a plane passing through the nucleus on which the probability of finding the electron is almost zero and is known as “Nodal Plane”. For p orbital, l = 1, m = +1, 0, -1 indicating that p orbitals have three different orientations and these p orbitals are designated as px, py and pz depending upon whether the electron density is maximum along the X, Y and Z-axis respectively. Thus, the three p-orbitals are at right angles to each other. The three p-orbitals belonging to a given energy level are ‘Degeenrate’ i.e. have equal energies. These positive and negative signs do not represent charges but indicate whether the orbital wave function is positive or negative in a particular region.
d-Orbitals:
For d orbitals, l = 2, m = -2, -1, 0, +1, +2 which shows that there are five d orbitals depending upon the axes between which or along which their electron clouds are concentrated. These five d orbitals are designated as dxy, dyz, dxz, dx2-y2 and dz2. Some important features of d-orbitals are as follows-
- All the five d orbitals of a given shell possess nearly the same energies but differ in their orientations in space.
- The dxy, dyz and dxz orbitals are exactly alike except that they lie between the axis X and Y; Y and Z and X and Z respectively and their shapes are clover-leaf.
- The dx2-y2 orbital is exactly like dxy except that it is rotated by an angle of 45° about Z-axis so that its lobes are directed along X and Y-axis. It is also a clover leaf-shaped.
- The dz2 orbital is symmetrical about the Z-axis in which part of orbital lying in the direction of a magnetic field is enlarged and the part perpendicular to it is contracted. It is dumb-bell in shape.
- These five d-orbitals can be divided into two sets. One set contains dz2 and dx2-y2 orbitals whose angular probability distributions are concentrated along the axial directions and the other set contains dxy, dyz and dxz orbitals whose angular probability distributions are maximum at an angle of 45° to the axial directions.
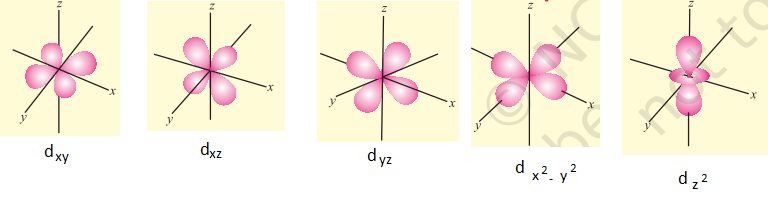
Difference between s, p and d orbitals:
| s orbital | p orbital | d orbital |
|---|---|---|
| s orbitals are spherically symmetrical. | p orbitals are dum-bell in shape. | d orbitals are clover-leaf and dum-bell in shape. |
| s orbitals are non-directional. | p orbitals are directional in nature. | d orbitals are also directional in nature. |
| s orbital is only of one-type. | p orbitals are of three types (px, py and pz). | d orbitals are of five types (dxy, dyz, dxz, dx2-y2 and dz2). |
| s orbital can accommodate a maximum of two electrons. | p orbital can accommodate a maximum of six electrons. | d orbital can accommodate a maximum of ten electrons. |
| For a given shell, s orbital is comparatively of lower energy. | p orbitals are comparatively of higher energy. | d orbitals are also of comparatively higher energy. |









Comments (No)