Arrhenius Equation:
Quantitatively, the effect of temperature on the rate of reaction and hence on the rate constant (k) was proposed by Arrhenius in 1889 called Arrhenius Equation. This equation is-
| k = Ae-Ea/RT |
Where A = Frequency Factor, Ea = Activation Energy, R = Gas Constant, T = Temperature
In this equation, the factor e-Ea/RT gives the fraction of molecules having energy equal to or greater than the activation energy (Ea).
Taking log to both sides of the above equation-
| 2.303 log k = 2.303 log (Ae-Ea/RT) = (2.303 log A) – (Ea/RT) ⇒ log k = log A – (Ea/2.303RT) = – (Ea/2.303R) (1/T) + log A ……….(I) |
Equation (I) resembles with equation of straight line, y = mx + C.
So when log k is plotted versus 1/T, we get a straight line as shown. The intercept of this line on the y-axis is equal to log A and the slope of line is equal to – Ea/2.303R.
| ∴ Slope = – Ea/2.303R |
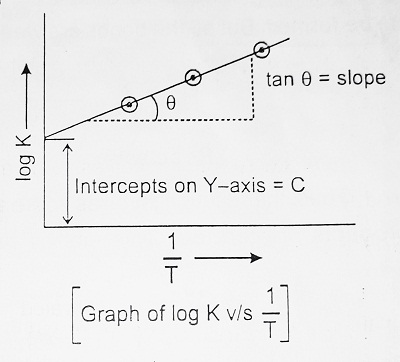
So, knowing the slope of equation and gas constant ‘R’ activation energy is calculated. It is the application of the Arrhenius Equation. It can alternatively be calculated by measuring two rate constants (k1) and (k2) at two temperatures T1k and T2k.
| log k1 = log A – (Ea/2.303RT1) and log k2 = log A – (Ea/2.303RT2) ∴ log k2 – log k1 = [log A – (Ea/2.303RT2)] – [log A – (Ea/2.303RT1)] = (Ea/2.303RT1) – (Ea/2.303RT2) or log (k2/k1) = Ea/2.303R (1/T1 – 1/T2) = Ea/2.303R [(T2 – T1)/T1T2] |









Comments (No)