Table of Contents
Terms Connected with Wave Motion:
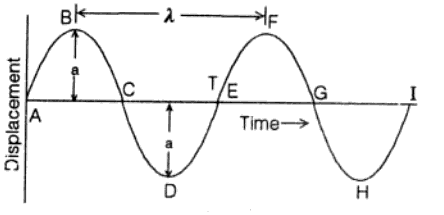
(1) Amplitude- The amplitude of a wave is the maximum displacement through which a vibrating particle of the medium undergoes on either side of its mean position of rest is called the amplitude. In the above figure, the magnitude of the maximum displacement “a” is represented as the amplitude of the wave.
(2) Time Period- It is defined as the time taken by the particle to complete one vibration about its mean position. As one vibration is equivalent to one wavelength, therefore, time period of a wave is equal to the time taken by the wave to travel a distance equal to one wavelength. It is denoted by T.
(3) Frequency- The number of vibrations made by a particle of the medium in one second is called the frequency of a wave. It is also the reciprocal of the time period T, i.e.
| Frequency = ν = 1/T |
(4) Wavelength- It is defined as the distance between the two nearest oscillating particles of the medium which are in the same phase of vibration. The distance is measured along the direction of propagation of the wave. In the above figure, λ is the wavelength of a wave. In a transverse wave, the distance between two successive crests or two successive troughs is called the wavelength of a transverse wave. Similarly, in a longitudinal wave, the distance between the two successive compressions or between the two successive rarefactions is called the wavelength of a longitudinal wave.
(5) Wave Speed- The distance traveled by the wave in one second is called wave speed. It is denoted by V.
(6) Phase- The phase of a vibrating particle of the medium at any instant represents the position and direction of motion of the particle at that instant. If during the propagation of a wave, two particles of the medium are in the same direction and at the same distance from their mean position of rest then they are said to be in the same phase. In the above figure, particles B and F are in the same phase. Similarly, particles A, E, and I are also in the same phase. The phase of vibration of various particles of the medium varies with the positions of the particles.
(7) Wave Form- The wave form is a picture of the instantaneous positions of various vibrating particles of the medium at a particular instant. The above figure represents a wave form.
Relation Between Frequency, Wave Speed, and Wavelength:
During the propagation of a wave, let a particle of the medium oscillate with frequency ν and travel a distance λ in a time T, where T is the time period and λ is the wavelength. Thus,
| Horizontal distance covered in T sec = λ ∴ Horizontal distance covered in one sec = λ/T The distance covered in one second is the wave speed of the wave. ∴ V = λ/T, or V = νλ [∵ ν = 1/T] |
Numericals:
| Example- A tuning fork vibrates with a frequency of 200. If the speed of sound is 301.5 m/sec, find the wave length and the distance, which the sound travels during the time the fork makes 40 vibrations. Solution- Here, Frequency, ν = 200 Hz Speed of sound, V = 301.5 m/sec Wave length, λ = ? Distance, x = ? We know that- V = νλ ⇒ 301.5 = 200 λ ⇒ λ = 301.5/200 = 1.51 m This is the distance that the sound travels in one vibration. In 40 vibrations, x = 40 x 1.51 = 60.4 m |
| Example- A private clinic uses an ultrasonic scanner to locate tumors in a cell. What is the wavelength of sound in a cell in which the speed of sound is 1.7 km/sec? The operating frequency of the scanner is 4.2 MHz. Solution- Here, Speed of sound, V = 1.7 km/sec = 1.7 x 103 m/sec Frequency of the scanner, ν = 4.2 MHz = 4.2 x 106 Hz Wave length, λ = ? We know that- V = νλ ⇒ 1.7 x 103 = 4.2 x 106 λ ⇒ λ = (1.7 x 103) / (4.2 x 106) ⇒ λ = 4.0 x 10-4 m Therefore, the wavelength of sound in a cell is 4.0 x 10-4 m. |









Comments (No)