Superposition of Two Magnetic Fields

Superposition of Two Magnetic Fields:

The magnetic field B is a vector quantity. If at a particular place two magnetic fields superimpose, the resultant field can be obtained by the usual vector methods. We shall discuss below two important cases of superposition of magnetic fields.

(1) Neutral Points- Figure shows the lines of force due to the resultant field of the earth and the magnet placed in the magnetic meridian with its N-pole pointing northwards.

Along the magnetic equator, the fields of the magnet B_F and the earth’s field B_H point in opposite directions. The magnetic field B_F of the magnet decreases as we go away from the magnet, but the field of Earth B_H is uniform in a small region under consideration.

Therefore, at some points marked as X in the below figure. The horizontal component of the field of the earth is exactly neutralized by the field of the magnet. These points are called neutral points.

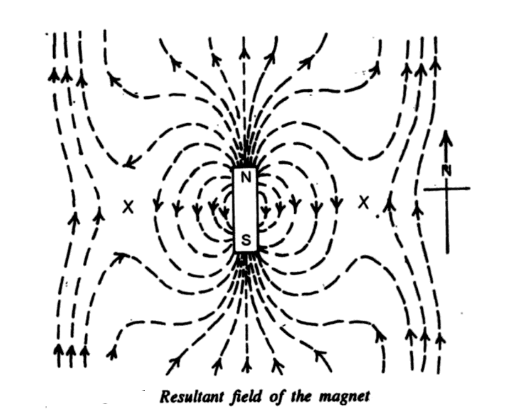
If the bar magnet is placed in the magnetic meridian with the N-pole pointing toward the north neutral points are obtained on either side of the magnet on its equatorial line, but if it is placed with N-pole pointing towards the south then the neutral points are obtained on the axis the magnet. If the field due to the magnet alone at the neutral point is B_F, then since this field just neutralizes the earth’s field B_H, we have

(2) Tangent Law- Suppose the magnet of length 2l (= L), pole strength Q_m and magnetic moment p_m is suspended in a region where there are two uniform magnetic fields B_F and B_H respectively at right angles to each other.

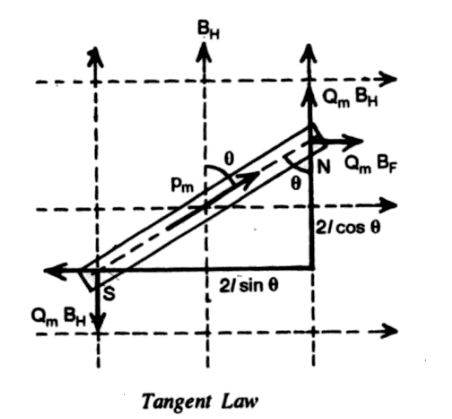
Due to the field B_H, the magnet experiences a couple which tends to bring the magnet in the direction of B_H. This couple is called a restoring couple and

Moment of restoring couple = p_mB_Hsinθ ……….(i)

where θ is the angle that the magnet makes with the direction of B_H.

Again, due to the field B_F, the magnet experiences a couple that tends to deflect the magnet from the original position parallel to B_F. This couple is known as the deflecting couple and

Moment of the deflecting couple = p_mB_Fcosθ ……….(ii)

If the suspended magnet is in equilibrium then the deflecting couple must have been balanced by the restoring couple, hence

The above relation gives the equilibrium orientation of a magnet suspended in a region where there are two mutually perpendicular fields and is the basis of tangent law which can be stated as follows:

When a magnet is suspended in two uniform perpendicular fields B_H and B_F, the tangent of the angle of deflection of the magnet with respect to one field B_H is the ratio B_F/B_H. This statement is known as tangent law.

Alternatively, the relation (iii) can be obtained by finding the direction of the resultant field by the law of parallelogram of vectors. Since the resultant field makes an angle θ with B_H such that tanθ = B_F/B_H, the freely suspended magnet will be in equilibrium in this direction.