Applications on Sets:
Consider two non-empty intersecting sets A and B. If we separately count the elements of A and B, then the elements contained in the portion A ∩ B will be counted twice. But in counting the elements of A ∪ B, the elements in portion A ∩ B is to be counted once only. If n (A ∪ B) denotes the number of elements in A ∪ B, then n (A ∪ B) = n(A) + n(B) – n (A ∩ B) [Fig. a].
In [Fig. b], the regions A – B, B – A and A ∩ B have been shown separately.
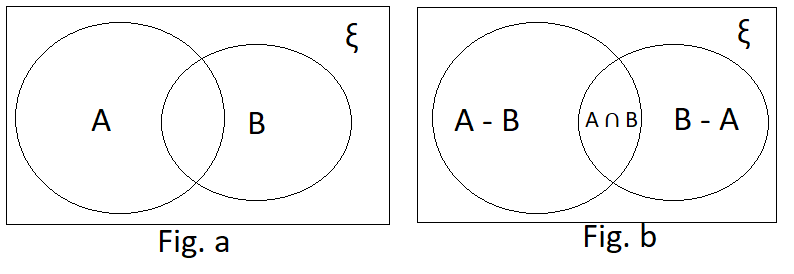
Obviously,
| n (A ∪ B) = n (A – B) + n (B – A) + n (A ∩ B), where n (A – B) = n (A) – n (A ∩ B) and n (B – A) = n (B) – n (A ∩ B) |
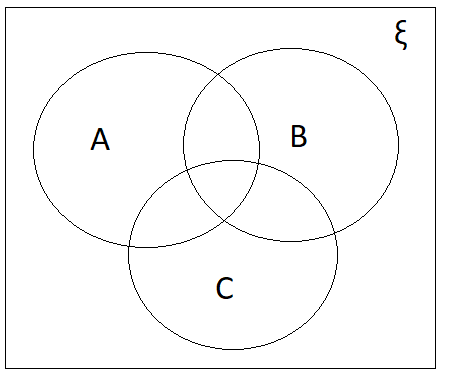
For any three sets A, B and C, we have
| n (A ∪ B ∪ C) = n(A) + n(B) + n (C) – n (A ∩ B) – n (B ∩ C) – n (A ∩ C) + n (A ∩ B ∩ C) Proof- n (A ∪ B ∪ C) = n [(A ∪ B) ∪ C] = n (A ∪ B) + n (C) – n [(A ∪ B) ∩ C] = n (A ∪ B) + n (C) – n [(A ∩ C) ∪ (B ∩ C)] = n (A) + n (B) – n (A ∩ B) + n (C) – [n (A ∩ C) + n (B ∩ C) – n {(A ∩ C) ∩ (B ∩ C)}] = n(A) + n(B) + n (C) – n (A ∩ B) – n (B ∩ C) – n (A ∩ C) + n (A ∩ B ∩ C) |
| Example- In a class of 40 students, 18 play cricket and 12 play football. It was found that 8 of them play both. Using algebra of sets find the number of students who play neither. Solution- Let F and C represent the set of students who play football and cricket respectively such that- n (F) = 12 n (C) = 18 n (F ∩ C) = 8 Now, n (F) + n (C) = n (F ∪ C) + n (F ∩ C) ⇒12 + 18 = n (F ∪ C) + 8 ⇒ 30 – 8 = n (F ∪ C) ⇒ n (F ∪ C) = 22 Therefore, the number of students who at least play one of the two games is 22. Thus, the number of students who play neither of the games = 40 – 22 = 18. |
| Example- In a group of 48 people, 22 drink tea but not coffee and 34 drink tea. Calculate how many drinks both, and how many drink coffee but not tea. Solution- Let T and C represent the set of persons who drink tea and coffee respectively. n (T ∪ C) = 48 n (T) = 34 n (T ∩ C’) = 22 Now, n (T ∩ C’) = 22 ⇒ n (T) – n (T ∩ C) = 22 ⇒ 34 – n (T ∩ C) = 22 ⇒ n (T ∩ C) = 12 Now, n (T) + n (C) – n (T ∪ C) = n (T ∩ C) ⇒ 34 + n (C) – 48 = 12 ⇒ n (C) – 14 = 12 ⇒ n (C) = 26 Now, the number of persons who drink both = n (T ∩ C) = 12. Number of person who drink coffee but not tea = n (C) – n (T ∩ C) = 26 – 12 = 14. |









Comments (No)