Table of Contents
Trigonometric Ratios of Some Standard Angles:
In the case of two similar right-angled triangles, the ratios of the corresponding sides are the same. So, the trigonometric ratios with respect to equal acute angles are also the same irrespective of the lengths of the sides. Thus, for an acute angle of any magnitude, one can determine its trigonometrical ratios by drawing a right triangle with one of its angles equal to the given acute angle.
Trigonometric Ratios of π/4:
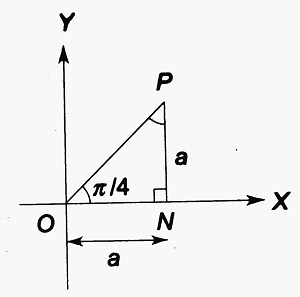
Let the revolving line OP starting from the initial position OX trace out ∠XOP = π/4 in the positive (anticlockwise) direction. From P, PN is drawn perpendicular to OX. Then, ∠NOP = π/4.
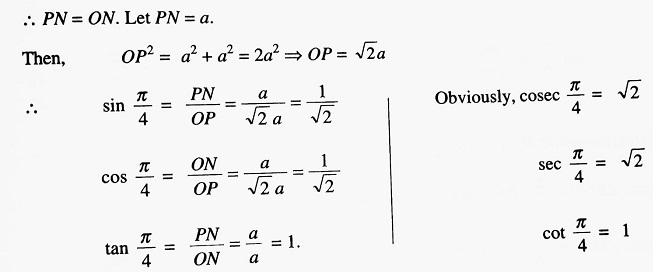
Trigonometric Ratios of π/6:
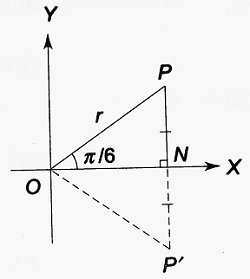
Let ∠XOP = π/6. PN is drawn perpendicular to OX, and is produced upto P’ such that NP’ = PN.
| Then, △PON ≅ △P’ON ∴ ∠P’ON = π/6, ∠OPN = π/3 Obviously, △POP’ is equilateral. ∴ OP = PP’ = r ⇒ PN = r/2 |

Trigonometric Ratios of π/3:
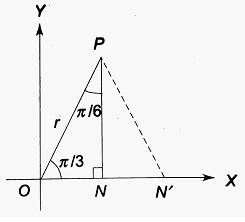
Here, ∠XOP = π/3. PN is drawn perpendicular to OX.
Then, ∠OPN = π/6. ON is produced upto N’ such that ON = NN’.
| Clearly, △ONP ≅ △N’NP ∴ ∠NN’P = π/3 and ∠N’PN = π/6 ∴ △OPN’ is equilateral ∴ ON = 1/2 ON’ = 1/2 OP = 1/2 r ∴ PN2 = OP2 – ON2 = r2 – (r/2)2 = r2 – r2/4 = 3r2/4 |
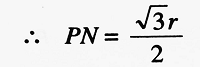

Trigonometric Ratios of 0 and π/2:
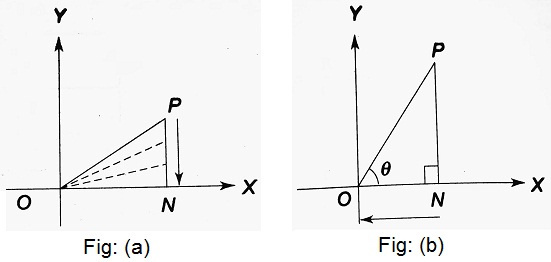
Let the revolving line OP, starting from OX, trace out a very small angle XOP = θ in the anticlockwise direction. From P, PN is drawn perpendicular to OX. If the point P is very close to N, then PN → 0, OP → ON and θ → 0 [Fig: (a)].
| ∴ sin 0 = PN/ON = 0/OP = 0 cos 0 = ON/OP = ON/ON = 1 tan 0 = PN/ON = 0/OP = 0 Obviously, cosec 0 = ON/PN = OP/0, undefined sec 0 = 1 cot 0 = ON/PN = OP/0, undefined |
Now, consider that the rotating line OP, starting from OX, trace out ∠XOP = θ, which is very nearly equal to π/2 in the anticlockwise direction.
Now, from P, PN is dropped perpendicular to OX. It is clear from [fig (b)] that as the angle θ approaches π/2, N approaches 0, PN → OP and ON → 0.
| ∴ sin π/2 = PN/OP = OP/OP = 1 cos π/2 = ON/OP = 0/OP = 0 tan π/2 = PN/ON = OP/0, undefined Obviously, cosec π/2 = 1 sec π/2 = OP/ON = OP/0, undefined and cot π/2 = ON/PN = 0/OP = 0 |
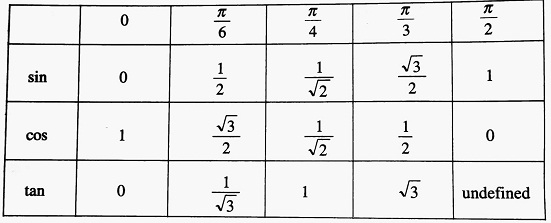
The table shows the values of trigonometric ratios for the standard angles 0, π/6, π/4, π/3 and π/2.
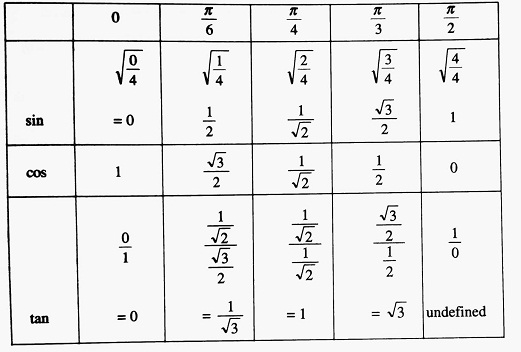
A handy method of determining the values of the t-ratios for the standard angles is discussed below.
The first five whole numbers 0 to 4 are written below the circular measures 0, π/6, π/4, π/3 and π/2 respectively along the row for the values of sin θ. All these numbers are divided by 4 and then the positive square roots of the resulting numbers are taken as the values of sin θ. The values thus obtained for sin θ are then written in the reverse order to get the values of cos θ. Finally, the values of sin θ are divided by the corresponding values of cos θ to get the values of tan θ.









Comments (No)