Wheat Stone Bridge Principle:
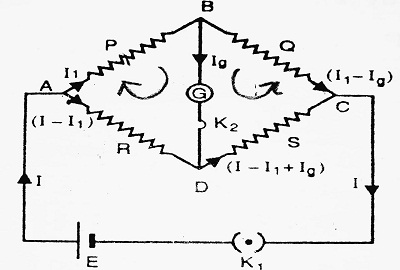
It states that if four resistances P, Q, R and S are arranged to form a bridge as shown, with a cell E and Key K1 connected between the points A and C, and a galvanometer G and Key K2 between the points B and D, then on closing K1 first and K2 later on if galvanometer shows no deflection, then the bridge is balanced.
| In that case, P/Q = R/S |
Proof: Press the Key K1 first and then K2, current I flow through the circuit.
At point A: I1 current flows through resistance P and (I – I1) current flows through R.
At point B: Ig current flows through galvanometer G and (I1 – Ig) current flows through Q.
At point D: (I – I1) is coming from R and Ig current is coming from G. Hence total current at D is (I – I1 + Ig) which flows through S as shown.
At point C: (I1 – Ig) current is coming from Q and (I – I1 + Ig) current is coming from S. Hence total current at C is I which flow through the circuit as shown.
Apply Kirchoff’s loop law to loop ABDA,
| I1P + IgG – (I – I1) R = 0 |
The value of R is adjusted such that the galvanometer shows no deflection i.e. Ig = 0.
| ⇒ I1P – (I – I1) R = 0 ⇒ I1P = (I – I1) R ………………(I) |
Apply Kirchoff’s loop law to loop BCDB,
| (I1 – Ig) Q – (I – I1 + Ig) S – Ig G = 0 |
The value of R is adjusted such that the galvanometer shows no deflection i.e. Ig = 0.
| (I1 – 0) Q – (I – I1 + 0) S – 0 = 0 ⇒ I1Q – (I – I1) S = 0 ⇒ I1Q = (I – I1) S ……………..(II) |
Divide (I) by (II),
| I1P / I1Q = (I – I1) R / (I – I1) S ⇒ P/Q = R/S |









Comments (No)