Internal Bisector of an Angle of a Triangle:
Let us construct a triangle ABC with its two sides AB and AC as 5 cm and 7 cm respectively and the included angle BAC = say, 50°. Now let us draw the bisector of ∠BAC meeting BC at D. We now measure BD and CD and find BD/CD. We observe that BD/CD = 5/7 = AB/AC.
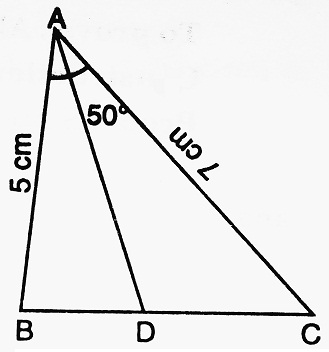
In other words, the bisector of an angle of the triangle divides the opposite side in the ratio of the sides including the angle. We can repeat this activity by drawing several such triangles and drawing the bisector of an angle. Every time we shall obtain the same result. Thus, we observe-
Theorem 1: The internal bisector of an angle of a triangle divides the opposite side internally in the ratio of the sides containing the angle.
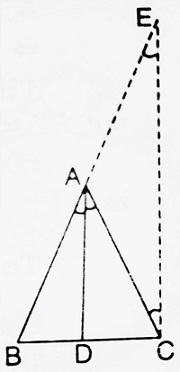
| Given: A △ABC is which the bisector of ∠BAC intersects BC in D. To prove: BD/DC = AB/AC Construction: Draw CE || DA to meet BA produced in E. Proof: In △EBC, since DA || CE, ∴ by Thales Theorem, we can write BD/DC = BA/AE ……….(i) Again, since CE || DA, ∴ ∠CAD = ∠ACE (alternate angles) ……….(ii) and ∠BAD = ∠AEC (corresponding angles) ……….(iii) But ∠BAD = ∠CAD (given) ……….(iv) ∴ (ii), (iii) and (iv) ⇒ ∠ACE = ∠AEC ∴ In △ACE, AC = AE (Equal angels have opposite sides equal) ……….(v) ∴ (i) and (v) imply that BD/DC = BA/AE = AB/AC Hence the result is proved. |
Theorem 2: (Converse of theorem 1). In a triangle ABC, if D is a point on BC such that BD/DC = BA/AC, prove that AD is the bisector of ∠A.
or
In a triangle ABC, if D is a point on BC such that D divides BC in the ratio AB : AC, then AD is the bisector of ∠A.
or
If a line through one vertex of a triangle divides the opposite sides in the ratio of the other two sides, then the line bisects the angle at the vertex.
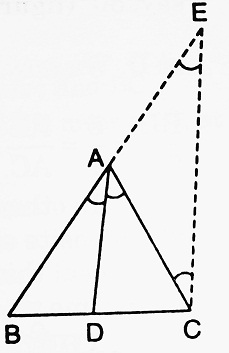
| Given: A △ABC in which a line through A meets BC in D such that BD/DC = BA/AC. To prove: AD bisects ∠BAC. Construction: Draw CE || DA to meet BA produced in E. Proof: Since DA || CE (Construction) ∴ ∠BAD = ∠AEC (Corresponding angles) ……….(i) and ∠CAD = ∠ACE (Alternate angles) ……….(ii) In △BCE, we have DA || CE, ∴ By Thales Theorem, we get BD/DC = BA/AE ……….(iii) Also, we are given that BD/DC = AB/AC ……….(iv) ∴ (iii) and (iv) ⇒ AC = AE, Now consider △ACE, we have AC = AE, ⇒ ∠ACE = ∠AEC (Opposite angles of equal sides are equal) ……….(vi) ∴ From (i), (ii) and (vi), we get, ∠BAD = ∠CAD ⇒ AD bisects ∠BAC. |
Theorem 3: The external bisector of an angle of a triangle divides the opposite side externally in the ratio of the sides containing the angle.
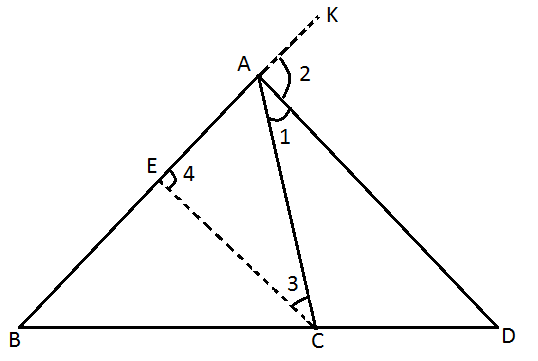
| Given: A △ABC in which AD is the bisector of the exterior ∠A and intersects BC produced in D. To prove: BD/CD = AB/AC Construction: Draw CE || DA meeting AB in E. Proof: Since CE || DA and AC intersect them, ∴ ∠1 = ∠3 ……….(i) Also, CE || DA and BK intersect them, ∴ ∠2 = ∠4 ……….(ii) But ∠1 = ∠2 [AD is the bisector of ∠CAK ∴ ∠1 = ∠2] ∴ ∠3 = ∠4 [from (i) and (ii)] Now in △ACE, we have ∠3 = ∠4 ⇒ AE = AC [∵ Sides opposite to equal angles in a △ are equal] ……….(iii) Now in △BAD, we have EC || AD ∴ BD/CD = BA/EA [Using corollary of basic proportionality theorem] ⇒ BD/CD = AB/AE [∵ BA = AB and EA = AE] ⇒ BD/CD = AB/AC [∵ AE = AC from (iii)] |









Comments (No)