The Cosine Formulae:
In △ABC with BC = a, CA = b and AB = c,
(i) cos A = (b2 + c2 – a2)/2bc (ii) cos B = (c2 + a2 – b2)/2ca (iii) cos C = (a2 + b2 – c2)/2ab
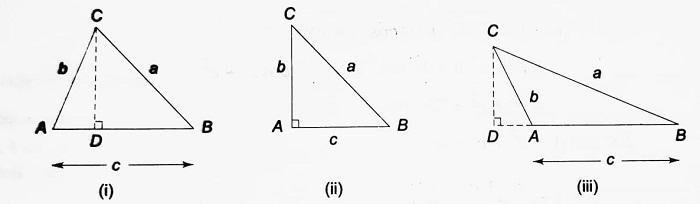
Proof- The proofs of all three formulae are similar. Let us take the first one. We consider three different types of △ABC- (i) acute-angled (ii) right-angled at A and (iii) obtuse-angled at A.
Case (i):
| CD is drawn perpendicular to AB, In △CAD, CD/AC = sin A [Fig. (i)] ∴ CD = AC sin A = b sin A Now, DB = c – AD = c – (AD/AC)AC = c – b cos A Now, in right-angled △CDB, BC2 = CD2 + BD2 ⇒ a2 = (b sin A)2 + (c – b cos A)2 ⇒ a2 = b2 sin2 A + c2 – 2bc cos A + b2 cos2 A ⇒ a2 = b2 (sin2 A + cos2 A) + c2 – 2 bc cos A ⇒ a2 = b2 + c2 – 2 bc cos A ∴ cos A = (b2 + c2 – a2)/2bc |
Case (ii):
| In △ABC, right-angled at A [Fig. (ii)] a2 = b2 + c2 = b2 + c2 – 2bc cos A (∵ cos A = cos 90° = 0) ∴ 2 bc cos A = b2 + c2 – a2 ∴ cos A = (b2 + c2 – a2)/2bc |
Case (iii):
| In △ABC, ∠A > 90°. CD is drawn perpendicular to BA produced [Fig. (iii)] ∴ In right-angled triangle CDA, CD/AC = sin A, ∴ CD = AC sin A = b sin A Also, AD/AC = cos A, ∴ AD = AC cos A = b cos A Now, in right-angled triangle CDB, BC2 = CD2 + DB2 ∴ a2 = (b sin A)2 + (b cos A + c)2 ⇒ a2 = b2 sin2 A + b2 cos2 A + 2bc cos A + c2 ⇒ a2 = b2 + c2 + 2bc cos A ∴ 2bc cos A = b2 + c2 – a2 ∴ cos A = (b2 + c2 – a2)/2bc |
From the above three cosine formulae, one can write-
| a2 = b2 + c2 – 2bc cos A b2 = c2 + a2 – 2ca cos B c2 = a2 + b2 – 2ab cos C |
Adding up, a2 + b2 + c2 = 2 (a2 + b2 + c2) – 2 (bc cos A + ca cos B + ab cos C)
⇒ a2 + b2 + c2 = 2 (bc cos A + ca cos B + ab cos C)
As a2 + b2 + c2 > 0, bc cos A + ca cos B + ab cos C > 0









Comments (No)