Table of Contents
Trigonometric Ratios of Submultiple Angles:
The angles (1/2) A, (1/3) A, ……etc., are called the submultiple angles of angle A. For all values of the angle A, we have-
| sin 2A = 2 sin A cos A = 2 tan A/(1 + tan2 A) cos 2A = cos2 A – sin2 A = 2 cos2 A – 1 = 1 – 2 sin2 A = (1 – tan2 A)/(1 + tan2 A) tan 2A = 2 tan A/(1 – tan2 A) cot 2A = (cot2 A – 1)/2 cot A |
Replacing 2A by θ in each of the above formulae, we get-
| sin θ = 2 sin θ/2 cos θ/2 = (2 tan θ/2)/(1 + tan2 θ/2) ……………(ii) cos θ = cos2 θ/2 – sin2 θ/2 = 2 cos2 θ/2 – 1 = 1 – 2 sin2 θ/2 = (1 – tan2 θ/2)/(1 + tan2 θ/2) ………(iii) tan θ = (2 tan θ/2)/(1 – tan2 θ/2) …………(iv) cot θ = (cot2 θ/2 – 1)/(2 cot θ/2) ………….(v) |
Again, for all values of the angle A, we can write-
| sin 3A = 3 sin A – 4 sin3 A cos 3A = 4 cos3 A – 3 cos A tan 3A = (3 tan A -tan3 A)/(1 – 3 tan2 A) |
Replacing 3A by θ in each of the above formulae, we get-
| sin θ = 3 sin θ/3 – 4 sin3 θ/3 ………….(vii) cos θ = 4 cos3 θ/3 – 3 cos θ/3 ………….(viii) tan θ = (3 tan θ/3 -tan3 θ/3)/(1 – 3 tan2 θ/3) …………..(ix) |
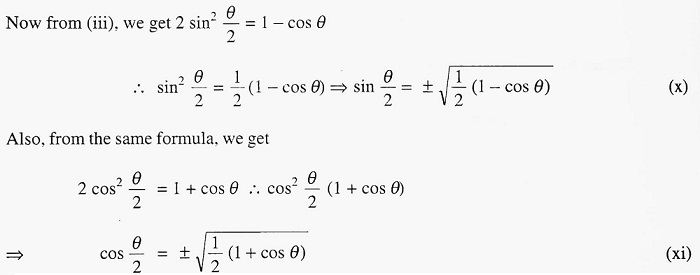
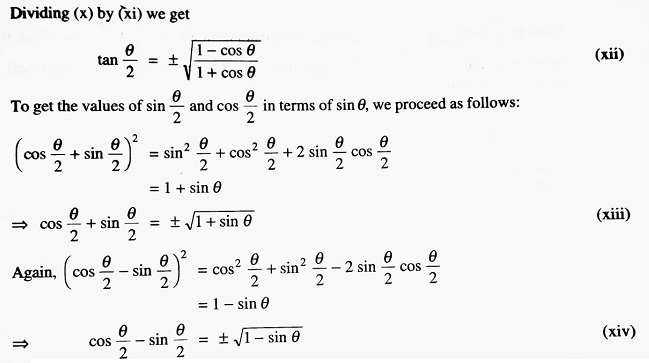
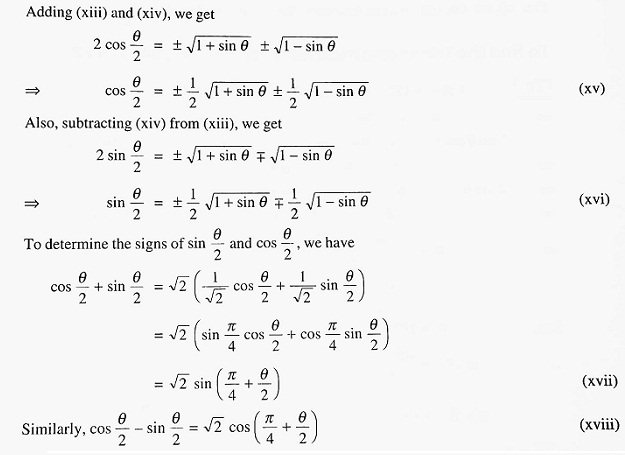
If θ is known, we can find out the respective quadrants in which (π/4 + θ) lies. Then, using the convention ‘all, sin, tan, cos’, we can determine the appropriate signs on the right side of equations (xvii) and (xviii).
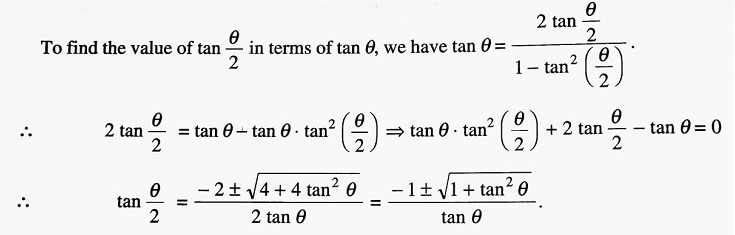
If the value of θ is known, we can find the quadrant in which θ/2 lies. Then, using the convention ‘all, sin,
tan, cos’, we can determine the appropriate sign of tan θ/2.
To find the Trigonometrical Ratios of 18°, 36°, 54° and 72°:


To find the Trigonometrical Ratios of 3°, 6°, 9° and 12°:

Using a similar method, we can find sines and cosines of 6°, 9°, 12° etc. Clearly, 6° = 36° – 30°, 9° = 45° – 36°, 12° = 30° – 18°, 21° = 36° – 15° and so on.
| Seebeck Effect | Applications Of Laser And Maser |
| Thomson Effect | Photoelectric Cell |
| Energy Bands in Solids | Applications of Photoelectric Effect |
| Diffraction Grating | Work, Energy and Power– NIOS |









Comments (No)