Intersection of a Line and a Circle:
Let us consider the line y = mx + c and the circle x2 + y2 = r2 (whose center is at the origin). For the point of intersection of the line and the circle, we have
| x2 + (mx + c)2 = r2 ⇒ x2 + m2x2 + 2mcx + c2 – r2 = 0 ⇒ (1 + m2) x2 + 2mcx + (c2 – r2) = 0 …………(i) which is a quadratic in x having two roots x1 and x2. The point of intersection are (x1, mx1 + c) and (x2, mx2 + c). The discriminant of the equation is (2mc)2 – 4(1 + m2) (c2 – r2) = 4m2c2 – 4(c2 + m2c2 – r2 – r2m2) = 4 { r2 (1+ m2) – c2 } = D |
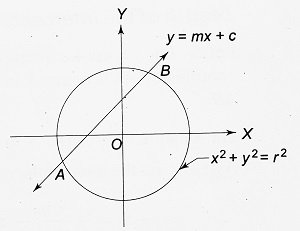
(i) If c2 < r2(1 + m2), then D > 0. The roots x1 and x2 are then real and distinct. In this case, the line y = mx + c intersects the circle x2 + y2 = r2 at two distinct points A and B as shown in the figure below. Here, r > | c / √(1 + m2) | i.e., the radius of the circle is more than the distance of the line from the center.
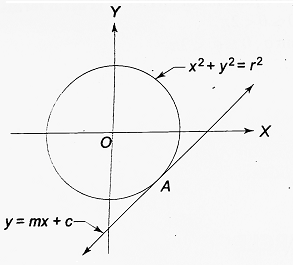
(ii) If c2 = r2(1 + m2), then D = 0. The roots x1 and x2 of equation (i) are equal. The line y = mx + c, in this case, intersects the circle x2 + y2 = a2 at two real and coincident points as shown in the figure below. Here, r = | c / √(1 + m2) i.e., the radius of the circle is equal to the distance of the line from the center.
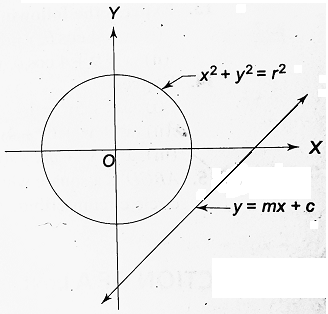
(iii) If c2 > r2(1 + m2), then D < 0. The roots x1 and x2 of equation (i) are imaginary. The line y = mx + c does not intersect the circle as shown in the figure below. In this case, r < | c / √(1 + m2) | i.e., the radius of the circle is less than the distance of the line from the center of the circle.
Length of the Intercepted Chord:
Let the line y = mx + c intersect the circle at two points A and B as shown in the figure. If the coordinates of points A and B be (x1, y1) and (x2, y2) respectively. The length of the chord is AB.
| For A and B, x2 + (mx + c)2 – r2 = 0 ⇒ (1 + m2) x2 + 2mcx + (c2 – r2) = 0 As x1, x2 are the roots of equation (i), we have x1 + x2 = -2mc / (1 + m2) and x1x2 = (c2 – r2) / (1 + m2) Now, A and B are points on y = mx + c ∴ y1 = mx1 + c and y2 = mx2+ c ∴ y1 – y2 = m (x1 – x2) Now, the length of the Chord AB = √[ (x1 – x2)2 + (y1 – y2)2 ] = √[ (x1 – x2)2 + m2 (x1 – x2)2 ] = √[ (x1 – x2)2 (1 + m2) ] = √[ { (x1 + x2)2 – 4x1x2 } (1 + m2) ]  |
Note:
| If AB = 0, then r2(1 + m2) – c2 = 0 ⇒ c = ± r √(1 + m2). In this case, A and B coincide and the line y = mx + c becomes a tangent to the circle x2 + y2 = r2. Thus, the condition of tangency of the line y = mx + c to the circle x2 + y2 = r2 is c = ± r √(1 + m2) or, r = | c / √(1 + m2) | i.e., the radius of the circle becomes equal to the length of the p[erendicular drawn from the center (0, 0) to the line y = mx + c. |
| Example 1: Find the coordinates of the point of intersection of the line x + √3 y + 7 = 0 and the circle x2 + y2 =10. Solution- The given equation of a line is, x + √3 y + 7 = 0 ⇒ x = -7 – √3 y ……….(i) and the equation of a circle is, x2 + y2 =10 ⇒ (-7 – √3 y)2 + y2 = 10 ⇒ 49 + 3y2 + 14√3 y + y2 = 10 ⇒ 4y2 + 14√3 y + 39 = 0 ⇒ y = [ -14√3 ± √{(14√3)2 – 4(4) (39)} ] / 2(4) ⇒ y = [ -14√3 ± √(588 – 624) ] / 8 ⇒ y = [ -14√3 ± 6i ] / 8 which gives imaginary values of y ∴ The line and circle do not intersect each other. |
| Example 2: For what value of c is the line y = 2x + c tangent to the circle x2 + y2 = 5? Solution- The given equation of a line is, y = 2x + c ⇒ 2x – y + c = 0 ………..(i) and the equation of a circle is, x2 + y2 = 5 ⇒ x2 + y2 = (√5)2 Center = (0, 0) Radius = √5 Since the line is tangent to the circle. The length of ⊥ from (0, 0) to the line, 2x – y + c = 0 is equal to the radius of a circle. ⇒ | 2(0) – 0 + c | / √[(2)2 + (1)2] = √5 ⇒ | c | / √5 = √5 ⇒ | c | = 5 ⇒ c = ± 5 |
| Example 3: Find the value of k for which the line x + y + k = 0 touches the circle x2 + y2 – 2x – 4y + 3 = 0. Solution- The given equation is, x + y + k = 0 and the equation of a circle is, x2 + y2 – 2x – 4y + 3 = 0 Center = (1, 2) and Radius (r) = √[ (1)2 + (2)2 – 3 ] = √2 Since the line touches the circle. ∴ The length of ⊥ from the point (1, 2) to the line x + y + k = 0 is equal to the radius of a circle. ⇒ | 1 + 2 + k | / √[ (1)2 + (1)2 ] = √2 ⇒ | 3 + k | = 2 ⇒ 3 + k = ±2 ⇒ 3 + k = 2 or 3 + k = -2 ⇒ k = -1 or k = -5 |









Comments (No)