Malus Law:
Statement: It states that the intensity of polarized light transmitted through the analyzer is directly proportional to the square of Cos θ where θ is the angle between the plane of the polarizer and the plane of the analyzer.
| i.e. I ∝ cos2 θ |
Proof: Let ‘a‘ be the amplitude of light transmitted through the polarizer and θ be the angle between the plane of the polarizer and the plane of the analyzer.
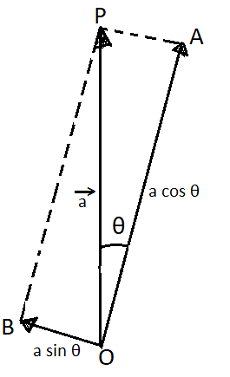
Resolve ‘a‘ into two components i.e., a cos θ along OA and a sin θ along OB. Clearly, a cos θ component will pass through the analyzer. We know,
| Intensity ∝ (Amplitude)2 ⇒ I ∝ (a cos θ)2 ⇒ I ∝ a2 cos2 θ ⇒ I = k a2 cos2 θ Put ka2 = Io = constant ⇒ I = Io cos2 θ ⇒ I ∝ cos2 θ |
| Sample Problem: Two polaroids are crossed to each other. Now one of them is rotated through 60°. What percentage of incident unpolarized light will pass through the system? Solution: Initially the polaroids are at 90°. When one is rotated through 60°, the angle between their transmission axes is 30° i.e., θ = 30°. Let Io be the intensity of the incident unpolarized beam. The intensity of the beam transmitted by the polarizer will be Io/2 as the other Io/2 is absorbed by the polaroid. The intensity of light transmitted by the analyzer will, therefore, be given by Io = Im cos2 θ where Im = Io/2, θ = 30°, hence Iθ = (Io/2) cos2 30° = (Io/2) (√3/2)2 ∴ (Iθ/Io) x 100 = (3/8) x 100 = 37.5% |









Comments (No)