Geometrical Representation of Fundamental Operations of Complex Numbers:
Consider two complex numbers z1 = a + i b and z2 = c + i d which are denoted by points P (a, b) and Q (c, d) on the complex plane. OP = | z1| and OQ = | z2 |. The parallelogram OPRQ is completed.
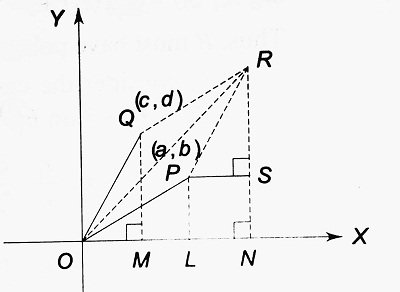
PL, QM and RN are drawn perpendiculars on OX. Also, PS is drawn perpendicular to RN (Above Figure).
| △OMQ ≅ △PSR (by AAS congruence) ∴ OM = PS = c QM = RS = d ∴ ON = OL + LN = OL + PS = a + c RN = RS + SN = RS + PL = b + d |
∴ R denotes the complex number whose real part is a + c and whose imaginary part is b + d. Thus, R represents the complex number-
| a + c + i (b + d) = (a + i b) + (c + i d) = z1 + z2 ∴ | z1 + z2 | = OR Now in △ ORP, OP + PR ≥ OR (equality holds only when O, P and R are collinear) ∴ OP + OQ ≥ OR ⇒ | z1 | + | z2 | ≥ | z1 + z2 | ………….(i) |
Thus, the sum of the moduli of two complex numbers is greater than or equal to the modulus of their sum.
| Now, let z and z2 be two complex numbers. Thus, from (i), we have | z | + | z2 | ≥ | z + z2 |. Replacing z + z2 by z1 i.e., z by z1 – z2, We get, | z1 – z2 | + | z2 | ≥ | z1 | ∴ | z1 – z2 | ≥ | z1 | – | z2 | ⇒ | z1 | – | z2 | ≤ | z1 – z2 | We now consider z1 and z2 in polar form, i.e., z1 = r1 (cos θ1 + i sin θ1) and z2 = r2 (cos θ2 + i sin θ2) ∴ z1 . z2 = r1r2 (cos θ1 + i sin θ1) (cos θ2 + i sin θ2) ⇒ z1 . z2 = r1r2 {(cos θ1 cos θ2 – sin θ1 sin θ2) + i (sin θ1 cos θ2 + cos θ1 sin θ2)} ⇒ z1 . z2 = r1r2 {cos (θ1 + θ2) + i sin (θ1 + θ2)}, which denotes a complex number whose modulus is r1r2 and whose argument is (θ1 + θ2). |
Thus, the product of two complex numbers is a complex number whose modulus is equal to the product of the moduli of the individual complex numbers and whose argument is the sum of the arguments of those complex numbers.
Let P and Q denote the two complex numbers z1 = r1 (cos θ1 + i sin θ1) and z2 = r2 (cos θ2 + i sin θ2) on the Argand plane such that | z1 | = OP = r1 and | z2 | = OQ= r2. The point R would then denote the complex number z1 . z2 such that OR = | z1 z2 | = r1r2 and arg (z1 z2) = arg (z1) + arg (z2) = θ1 + θ2 = ∠ROX.
Thus, R must have polar coordinates (r1r2, θ1 + θ2) (Fig. (a)).
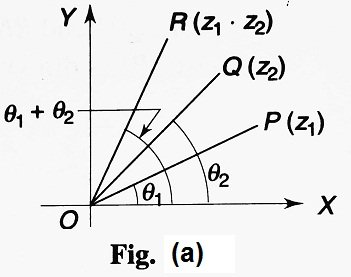
Now, consider the case of the division of two complex numbers z1 = r1 (cos θ1 + i sin θ1) and z2 = r2 (cos θ2 + i sin θ2).
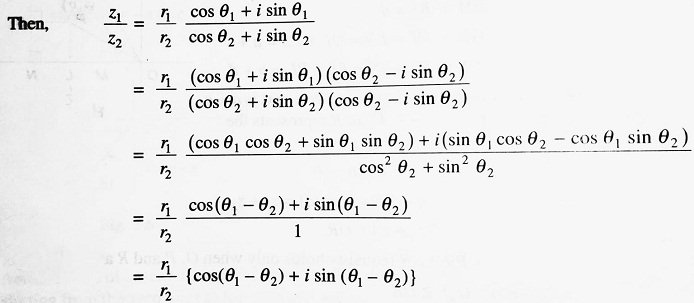
Obviously, the quotient z1/z2 is a complex number whose modulus is equal to the quotient of the moduli of the individual complex numbers z1 and z2 and whose argument is the difference of the two arguments θ1 and θ2. Thus, the quotient z1/z2 would be denoted by the point R on the complex plane having polar coordinates (r1/r2, θ1 – θ2) (Below Figure).

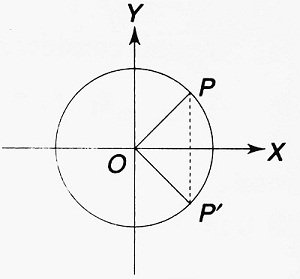
It has already been mentioned that the two complex numbers z = a + i b and z̄ = a – i b are conjugate to each other. On the complex plane if P denotes the complex number z(a, b) then P’ would denote z̄ (a, -b). (Below Figure)
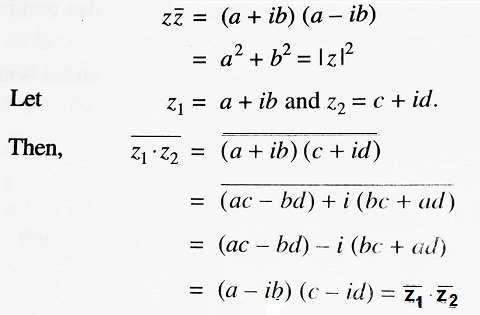
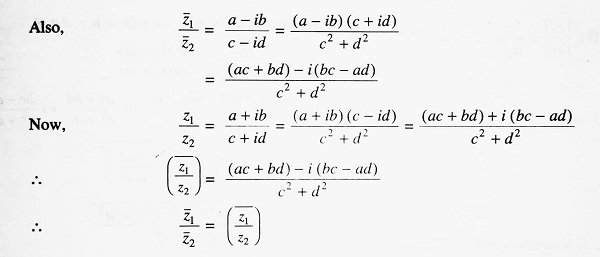








Comments (No)