Table of Contents
Trigonometric Ratios of Associated Angles:
You have already come to know about the trigonometric ratios of positive acute angles. Two perpendicular lines XOX’ and YOY’ divide the plane of the paper into four quadrants namely XOY, X’OY, X’OY’ and XOY’. The line OP, starting from the initial position or zero position OX, rotates in the anticlockwise direction to trace ou an angle of magnitude θ. If the line moves in the clockwise direction then the angle traced out by it is taken to be negative. In this section, we shall discuss the trigonometric ratios of an angle of any magnitude.
T-ratios of angle θ:
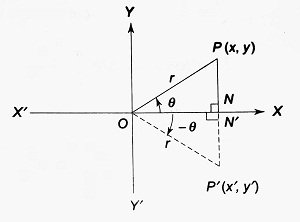
Let θ (0 < θ < π/2) be any real number. We construct angles of measures θ radian and -θ radian with vertices at the origin of the rectangular coordinate system and the initial arm along the positive X-axis. Let P(x,y) and P'(x’, y’) be equidistant points from the origin lying on the terminal arms of the angles θ and -θ respectively. Also, let OP = r. Then, OP’ = r.PN and P’N’ are drawn perpendiculars on OX.
| Now, △P’ON’ ≅ △PON (by AAS congruence) ∴ ON’ = ON and N’P’ = NP ∴ x’ = x and y’ = -y ∴ sin (-θ) = y’/r = -y/r = -sin θ, cos (-θ) = x’/r = x/r = cos θ, tan (-θ) = y’/x’ = -y/x = -tan θ Obviously cosec (-θ) = -cosec θ, sec (-θ) = sec θ and cot (-θ) = -cot θ |
T-ratios of angle π/2 – θ:
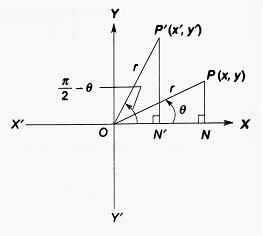
We consider a real number θ (0 < θ < π/2). Angles with measures θ radian and (π/2 – θ) radian are constructed with the vertices at the origin of the rectangular coordinate system and the initial arm along the positive X-axis. Points P(x,y) and P'(x’,y’) are taken equidistantly from the origin on the terminal arms of the two angles respectively. PN and P’N’ are drawn perpendiculars on OX.
| ∠P’ON’ = π/2 – θ, ∴ ∠OP’N’ = θ ∴ △P’ON’ ≅ △OPN (by AAS congruence) ∴ P’N’ = y’ = ON =x and ON’ = x’ = PN = y ∴ sin (π/2 – θ) = y/r = x/r = cos θ cos (π/2 – θ) = x’/r = y/r = sin θ tan (π/2 – θ) = y’/x’ = x/y = cot θ Obviously, cosec (π/2 – θ) = sec θ, sec (π/2 – θ) = cosec θ and cot (π/2 – θ) = tan θ |
T-ratios of angle π/2 + θ:
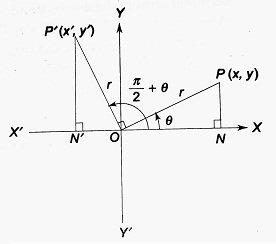
P(x, y) and P'(x’, y’) are equidistant points from the origin on the terminal arms of the angles θ and π/2 + θ with the same vertex O and the same initial arm along OX.
| △P’ON’ ≅ △OPN (by AAS congruence) ∴ ON’ = PN and P’N’ = ON ∴ x’ = -ON’ = -PN = -y and y’ = P’N’ = ON = x ∴ sin (π/2 + θ) = y’/r = x/r = cos θ cos (π/2 + θ) = x’/r = -y/r = -sin θ tan (π/2 + θ) =y’/x’ = x/(-y) = -cot θ Obviously, cosec (π/2 + θ) = sec θ, sec (π/2 + θ) = -cosec θ and cot (π/2 + θ) = -tan θ |
T-ratios of angle π – θ:
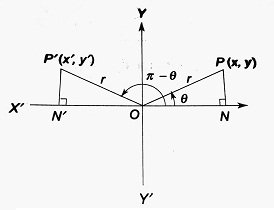
| Here, △P’ON’ ≅ △PON (by AAS congruence) ∴ ON’ = ON and P’N’ = PN ∴ x’ = -ON’ = -ON =-x and y’ = P’N’ = PN = y ∴ sin (π – θ) = y’/r = y/r = sin θ cos (π – θ) = x’/r = -x/r = -cos θ tan (π – θ) = y’/x’ = y/(-x) = -tan θ Clearly, cosec (π – θ) = cosec θ, sec (π – θ) = -sec θ and cot (π – θ) = -cot θ |
T-ratios of angle π + θ:
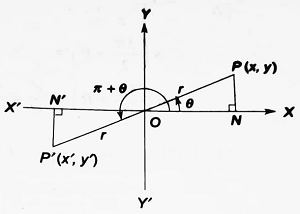
| In this case, △P’ON’ ≅ △PON (by AAS congruence) ∴ ON’ = ON and P’N’ = PN ∴ x’ = -ON’ = -ON =-x and y’ = -N’P’ = -PN = -y ∴ sin (π + θ) = y’/r = -y/r = -sin θ cos (π + θ) = x’/r = -x/r = -cos θ tan (π + θ) = y’/x’ = -y/(-x) = y/x = tan θ Clearly, cosec (π + θ) = -cosec θ, sec (π + θ) = -sec θ and cot (π + θ) = cot θ |
T-ratios of angle 3π/2 – θ:
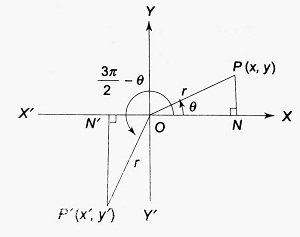
| Here, △P’ON’ ≅ △OPN (by AAS congruence) ∴ ON’ = PN and P’N’ = ON ∴ x’ = -ON’ = -PN = -y and y’ = -N’P’ = -ON =-x ∴ sin (3π/2 – θ) = y’/r = -x/r = -cos θ cos (3π/2 – θ) = x’/r = -y/r = -sin θ tan (3π/2 – θ) = y’/x’ = -x/(-y) = cot θ Clearly, cosec (3π/2 – θ) = -sec θ, sec (3π/2 – θ) = -cosec θ and cot (3π/2 – θ) = tan θ |
T-ratios of angle 3π/2 + θ:
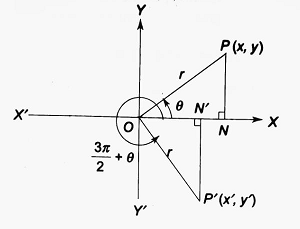
| Here, △P’ON’ ≅ △OPN (by AAS congruence) ∴ ON’ = PN and P’N’ = ON ∴ x’ = ON’ = PN = y and y’ = -P’N’ = -ON =-x ∴ sin (3π/2 + θ) = y’/r = -x/r = -cos θ cos (3π/2 + θ) = x’/r = y/r = sin θ tan (3π/2 + θ) = y’/x’ = -x/y = -cot θ Obviously, cosec (3π/2 + θ) = -sec θ, sec (3π/2 + θ) = cosec θ and cot (3π/2 + θ) = -tan θ |
T-ratios of angle 2π – θ:
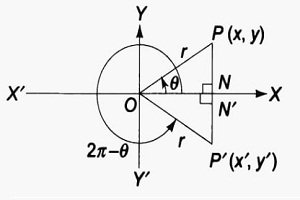
| Here, △P’ON’ ≅ △PON (by AAS congruence) ∴ ON’ = ON and P’N’ = PN ∴ x’ = ON’ = ON = x and y’ = -P’N’ = -PN =-y ∴ sin (2π – θ) = y’/r = -y/r = -sin θ cos (2π – θ) = x’/r = x/r = cos θ tan (2π – θ) = y’/x’ = -y/x = -tan θ Obviously, cosec (2π – θ) = -cosec θ, sec (2π – θ) = sec θ and cot (2π – θ) = -cot θ |
The following rules will help one to evaluate the trigonometric ratios in terms of those of standard angles between lying 0 and π/2.

(I) Any function of an angle (nπ ± θ) where n is any integer and θ being treated as acute, is numerically equal to the same function of θ, with sign depending on the quadrant in which the revolving line describing the angle terminates following the rule all-sin-tan-cos. For example, cos (5π + θ) = -cos θ. (The sign is ‘minus’ because of the fact that the revolving line describing the angle terminates in the 3rd quadrant where cos is negative, [Fig: (a)]).
(II) Any function of an angle [(2n + 1)π/2 ± θ], where n is any integer and θ being treated as acute, is numerically equal to cofunction of θ, with sign depending on the quadrant in which the revolving line terminates following the convention all-sin-tan-cos. Remember that sin and cos are cofunctions of each other. Also, tan and cot, as well as sec and cosec, are cofunctions of each other. Thus, sec (3π/2 + θ) = cosec θ. Here, cosec is the cofunction of sec and the sign is positive because the terminal line lies in the 4th quadrant where cos as well as sec are positive, [Fig: (b)].








Comments (No)