Table of Contents
Coordinate System in Three Dimensions:
We live in a world of three dimensions and so we should extend our knowledge of geometry to three-dimensional space. To specify the position of a point in space, we require three axes of reference- X-axis, Y-axis, and Z-axis.
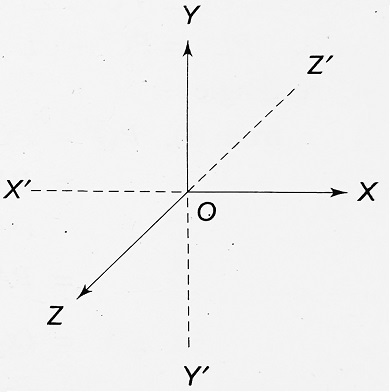
In the figure, X’OX, Y’OY, and Z’OZ are the three axes of references. The positive directions of the axes have been indicated by arrowheads. The axes are perpendicular to each other and so they are referred to as the rectangular axes. The point of intersection of the axes is the origin. In the figure, O is the origin.
Coordinates Planes:
Each pair of axes constitutes a plane. The X-axis and Y-axis are on a plane called the XY-plane. Similarly, the plane containing Y-axis and Z-axis is called the YZ-plane and the plane containing Z and X-axes is called the ZX-plane. The plane XOY, YOZ, and ZOX are known as coordinate planes. These planes divide the entire space into eight parts known as the octans.
Coordinates of a Point:
In order to specify the position of a point on a plane we require an ordered pair of real numbers. In three-dimensional space, we require a triplet of real numbers to describe a point. Each number denotes the distance of the point from a coordinate plane. Thus, if P be a point in space, its coordinates may be denoted by (x, y, z), where x denotes the distance of the point from the YZ-plane, y is the distance from the ZX-plane and z from the XY-plane. The ordered triplet of real numbers constitutes cartesian coordinates of the point P and is written as P (x, y, z).

Thus, in the figure, OA = x, OB = y, and OC = z. To have a clear idea about the geometry in space, the rectangular parallelepiped has been completed with OA, OB, and OC as coterminous edges through the origin O and P at the opposite vertex.
Distance Formula:
Let P (x1, y1, z1) and Q (x2, y2, z2) be two given points in space. Through P and Q, planes are drawn parallel to the coordinates planes to form a cuboid with the line segment PQ as one of its diagonals as shown in the figure. QL is perpendicular to the plane PCLA and PL lies in this plane. So, QL ⊥ PL. ∴ ∠PLQ = 90°.
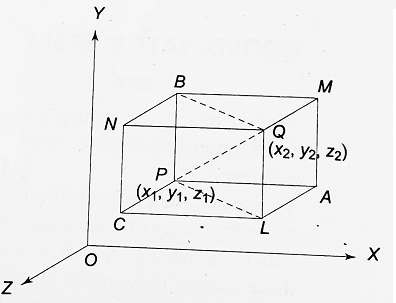
| ∴ in the right triangle PLQ, PQ2 = PL2 + QL2 ……….(i) Now, CL ⊥ PC ∴ ∠PCL = 90° ∴ PL2 = PC2 + CL2 = PC2 + PA2 (PCLA is a rectangle) ∴ from (i), PQ2 = PC2 + PA2 + QL2 ⇒ PQ2 = PA2 + PC2 + PB2 (∵ PLQB is a rectangle) ⇒ PQ2 = PA2 + PB2 + PC2 ⇒ PQ2 = (x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2 Thus, PQ = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2] Note: If one of the points is the origin and the coordinates of the other point P be (x, y, z), then the distance of P(x, y, z) from the origin is given by OP = √[(x – 0)2 + (y – 0)2 + (z – 0)2] = √[x2 + y2 + z2] |
Section Formula:
Coordinates of a point that divides the line segment joining two points in a given ratio. Let P (x1, y1, z1) and Q (x2, y2, z2) be the two given points. Let R (x, y, z) be the point that divides PQ internally in the ratio m : n, so that PR : RQ = m : n. PL, QM, and RN are drawn perpendicular to the ZX plane. Through R, SRT is drawn parallel to LNM to meet LP produced at S and QM at T as shown in the figure.
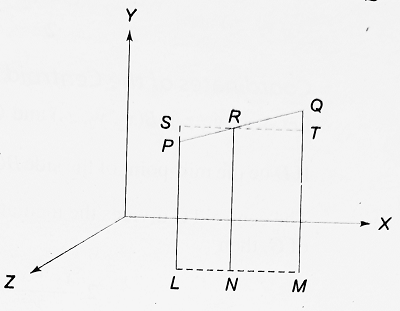
| Now, △SPR ~ △TQR ∴ SP/TQ = SR/RT = PR/RQ = m/n ∴ (y – y1)/(y2 – y) = (x – x1)/(x2 – x) = m/n ……….(i) So, (x – x1)/(x2 – x) = m/n ⇒ mx2 – mx = nx – nx1 ⇒ (m + n) x = mx2 + nx1 ⇒ x = (mx2 + nx1)/(m + n) Also, (y – y1)/(y2 – y) = m/n gives y = (my2 + ny1)/(m + n) Similarly, by drawing perpendiculars from P, R, and Q on the YZ plane, one can show that z = (mz2 + nz1)/(m + n) Thus, the coordinates of the point R are [(mx2 + nx1)/(m + n), (my2 + ny1)/(m + n), (mz2 + nz1)/(m + n)] |
Note:
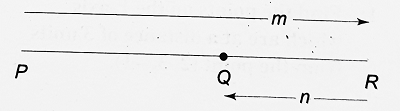
(i) If m : n is negative, then the segments PR and RQ have opposite directions and in that case, R divides PQ externally in the ratio m : n as shown in the figure.
(ii) To find out the ratio in which a given point divides the join of two given points, it is convenient to consider the ratio λ : 1. (instead of inviting two unknowns m and n). The coordinates of R then become [(λx2 + x1)/(λ + 1), (λy2 + y1)/(λ + 1), (λz2 + z1)/(λ + 1)].
(iii) If R divides PQ internally in the ratio 1 : 1, then R is the mid-point of PQ. In that case,
| x = (1.x2 + 1.x1)/(1 + 1) = (x1 + x2)/2, y = (1.y2 + 1.y1)/(1 + 1) = (y1 + y2)/2, z = (1.z2 + 1.z1)/(1 + 1) = (z1 + z2)/2 |
Thus, the coordinates of the mid-point of the line segment joining the points (x1, y1, z1) and (x2, y2, z2) are [(x1 + x2)/2, (y1 + y2)/2, (z1 + z2)/2].
Coordinates of the Centroid of a Triangle:
Let A (x1, y1, z1), B (x2, y2, z2), and C (x3, y3, z3) be the vertices of a given triangle as shown in the figure.
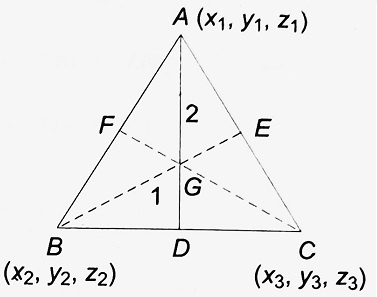
If D is the mid-point of the side BC, then the coordinates of D are [(x2 + x3)/2, (y2 + y3)/2, (z2 + z3)/2].
The centroid G divides the median AD internally in the ratio 2 : 1. If (x,
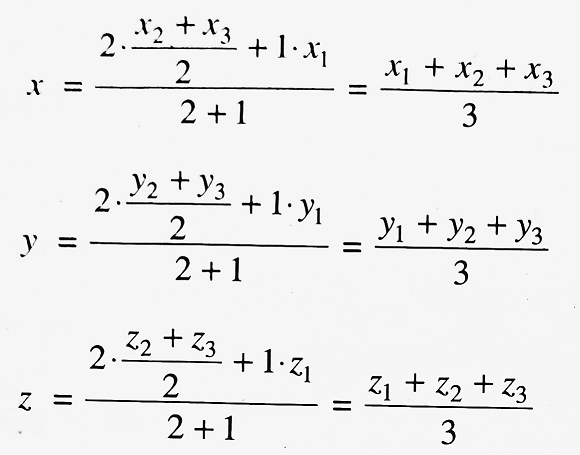
Examples:
| Example 1: By using the distance formula prove that A (3, -5, 1), B (-1, 0, 8), and C (7, -10, -6) are collinear. Solution- AB = √[(-1 – 3)2 + (0 + 5)2 + (8 – 1)2] ⇒ AB = √(16 + 25 + 49) ⇒ AB = √90 = 3√10 BC = √[(7 + 1)2 + (-10 – 0)2 + (-6 – 8)2] ⇒ BC = √(64 + 100 + 196) ⇒ BC = √360 = 6√10 and AC = √[(7 – 3)2 + (-10 + 5)2 + (-6 – 1)2] ⇒ AC = √(16 + 25 + 49) ⇒ AC = √90 = 3√10 Here, AB + AC = 3√10 + 3√10 = 6√10 = BC ∴ Points A, B, and C are collinear. |
| Example 2- Find the ratio in which the line segment joining (1, 2, 3) and (3, 4, -6) is divided by the XY plane. Solution- Let A (1, 2, 3) and B (3, 4, -6) be the two points. Let XY-plane divides the line AB in the ratio λ : 1 at P. Coordinates of P are [(3λ + 1)/(λ + 1), (4λ + 2)/(λ + 1), (-6λ + 3)/(λ + 1)] But P lines on XY-plane ∴ (-6λ + 3)/(λ + 1) = 0 ⇒ -6λ + 3 = 0 ⇒ λ = 1/2 ∴ XY plane divides AB internally in the ratio 1 : 2 |
| Example 3: L (3, 2, 0), M (5, 3, 2) and N (-9, 6, -3) are three points forming a triangle. LT, the bisectors of ∠MLN meets MN at T. Find the coordinates of T. Solution- LT is the bisector of ∠MLN ∴ MT/TN = LM/LN MT/TN = √[(5 – 3)2 + (3 – 2)2 + (2 – 0)2] / √[(-9 – 3)2 + (6 – 2)2 + (-3 – 0)2] ⇒ MT/TN = √(4 + 1 + 4) / √(144 + 16 + 9) = 3/13 ∴ Coordinates of T are [(-27 + 65)/(3 + 13), (18 + 39)/(3 + 13), (-9 + 26)/(3 + 13)] = (38/16, 57/16, 17/16) = (19/8, 57/16, 17/16) 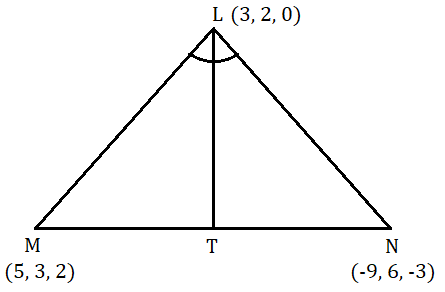 |
| Example 4: Find the point on the Y-axis which are at a distance of 3 units from the point (2, 3, -1). Solution- Let A (0, y, 0) be the point on the y-axis and let B (2, 3, -1) be the other point such that AB = 3 ⇒ √[(2 – 0)2 + (3 – y)2 + (-1 – 0)2] = 3 Squaring: ⇒ 4 + 9 + y2 – 6y + 1 = 9 ⇒ y2 – 6y + 5 = 0 ⇒ (y – 1) (y – 5) = 0 ⇒ y = 1 or y = 5 ∴ The required points are (0, 1, 0) and (0, 5, 0) |
| Example 5: Find the point in the XZ plane equidistant from the points (1, -1, 0), (2, 1, 2), and (3, 2, -1). Solution- Let the point on the XZ plane be P (x, 0, z). Here, A (1, -1, 0), B (2, 1, 2), and C (3, 2, -1) be the three points such that PA = PB = PC Now, PA = PB Squaring both sides, we get PA2 = PB2 ⇒ (x – 1)2 + (0 + 1)2 + (z – 0)2 = (x – 2)2 + (0 – 1)2 + (z – 2)2 ⇒ x2 + 1 – 2x + 1 + z2 = x2 + 4 – 4x + 1 + z2 + 4 – 4z ⇒ 2x + 4z = 7 ……….(a) Also, PB = PC Squaring both sides, we get PB2 = PC2 ⇒ (x – 2)2 + (0 – 1)2 + (z – 2)2 = (x – 3)2 + (0 – 2)2 + (z + 1)2 ⇒ x2 + 4 – 4x + 1 + z2 + 4 – 4z = x2 + 9 – 6x + 4 + z2 + 1 + 2z ⇒ 2x – 6z = 5 ……….(b) subtract (b) from (a) 2 x + 4z -2x + 6z = 7 – 5 ⇒ 10z = 2 ⇒ z = 1/5 Substitute z = 1/5 in equation (a) 2x + 4z = 7 ⇒ 2x + 4/5 = 7 ⇒ 10x + 4 = 35 ⇒ 10x = 31 ⇒ x = 31/10 ∴ Required point is (31/10, 0, 1/5) |









Comments (No)