Cube Roots of Unity:
Let us denote the cube roots of unity be z.
Then, z = (1)1/3 ⇒ z3 – 1 = 0 ⇒ (z – 1) (z2 + z + 1) = 0
When z – 1 = 0, z = 1 (real)
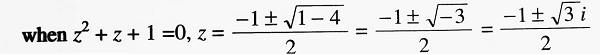
Thus, one of the cube roots of unity is real and the other two are conjugate complex numbers.
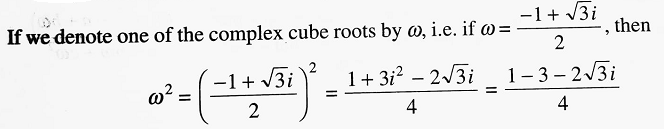
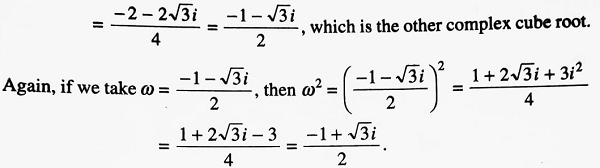
Thus, one of the complex cube roots is the square of the other. Hence, the three cube roots of unity are 1, ω and ω2.
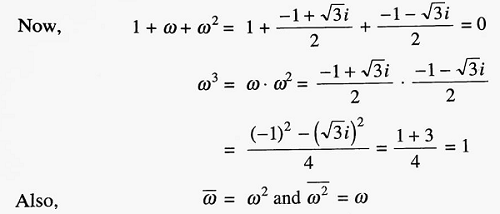
Properties of Cube Roots of Unity:
- Sum of the cube roots of unity is 0 that is 1 + ω + ω2 = 0.
- Product of the cube roots of unity is 1 that is 1 . ω . ω2 = ω3 = 1.
- Each complex cube root of unity is square of the other.
- Each complex cube root of unity is reciprocal of other i.e. ω = 1/ω2 or ω2 = 1/ω.
| Example- If α, β are the complex cube roots of unity then prove that α4 + β4 + 1/αβ = 0. Solution- The complex cube roots of unity are ω and ω2. Here, the complex cube roots are α and β. ∴ α = ω, β = ω2 Now, α4 + β4 + 1/αβ = ω4 + (ω2)4 + 1/ω.ω2 ⇒ α4 + β4 + 1/αβ = (ω3) ω + (ω3)2 ω2 + 1 ⇒ α4 + β4 + 1/αβ = ω + ω2 + 1 ⇒ α4 + β4 + 1/αβ = 0 |
| Example- If 1, ω and ω2 be the cube roots of unity then prove that (1 – ω + ω2) (1 – ω2 + ω4) (1 – ω4 + ω8)…………….to 2n factors = 22n. Solution- (1 – ω + ω2) (1 – ω2 + ω4) (1 – ω4 + ω8) (1 – ω8 + ω16)…………….2n factors = (1 – ω + ω2) (1 – ω2 + ω) (1 – ω + ω2) (1 – ω2 + ω)…………….2n factors = [(1 + ω2) – ω] [(1 + ω) – ω2] [(1 + ω2) – ω] [(1 + ω) – ω2]…………….2n factors = (-ω – ω) (-ω2 – ω2) (-ω – ω) (-ω2 – ω2)…………….2n factors = (-2ω) (-2ω2) (-2ω) (-2ω2)…………….2n factors = [(-2ω) (-2ω2)] [(-2ω) (-2ω2)]…………….n factor = (4ω3) (4ω3)…………….to n factor = (4) (4)…………….to n factor = 4n = (22)n = 22n |









Comments (No)