Tangents to a Circle

Table of Contents

Tangents to a Circle:

You know that if a line intersects a circle at two coincident points, then the line is called a tangent to the circle at the point of contact.

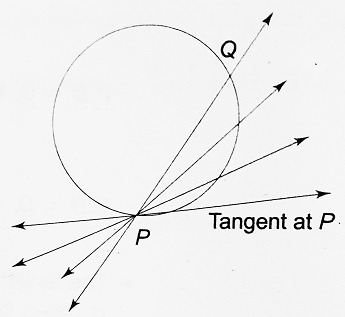
In the figure, the line PQ intersects the circle at P and Q. If the line PQ is now rotated about P in the clockwise direction as shown in the figure, then ultimately a position is reached when Q coincides with P. At this stage, the line becomes tangent to the circle at P. The point P is known as the point of tangency or the point of contact.

Equation of the Tangent to the Circle x² + y² = r² at (x₁, y₁):

Equation of the Tangent to the Circle at (x1, y1)

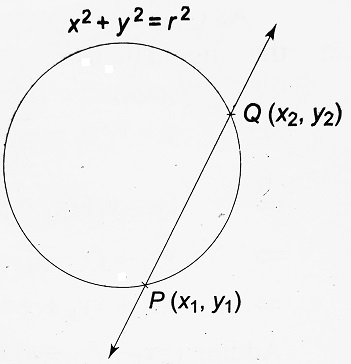
Let P be the point (x₁, y₁) on the circle x² + y² = r². We take a neighboring point Q (x₂, y₂) on the circle as shown in figure.

Thus, x₁² + y₁² = r² ……….(i)
and x₂² + y₂² = r² ……….(ii)

Equation to PQ is,
y – y₁ = [ (y₂ – y₁) / (x₂ – x₁) ] (x – x₁) ……….(iii)

From (i) and (ii), we get
x₂² – x₁² + y₂² – y₁² = 0
⇒ (x₂ + x₁) (x₂ – x₁) = – (y₂ + y₁) (y₂ – y₁)
⇒ (y₂ – y₁) / (x₂ – x₁) = – (x₁ + x₂) / (y₁ + y₂)

∴ Equation to PQ becomes, y – y₁ = – [ (x₁ + x₂) / (y₁ + y₂) ] (x – x₁)

As Q → P, x₂ → x_1, and y₂ → y₂, and the line PQ becomes a tangent to the circle at P. Thus, the equation to the tangent to the circle x² + y² = r² at P is

y – y₁ = – (2x₁/2y₁) (x – x₁)
⇒ x₁ (x – x₁) + y₁ (y – y₁) = 0
⇒ xx₁ + yy₁ = x²₁ + y²₁ = r² (∵ x² + y² = r²)

Equation of the Tangent to the Circle x² + y² + 2gx + 2fy + c= 0 at the point (x₁, y₁):

Equation of the Tangent to the Circle at the point

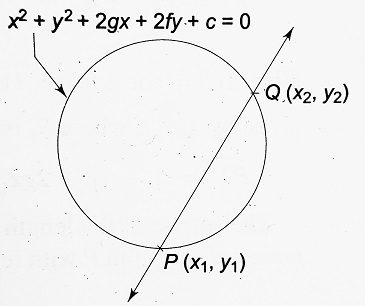
Let P be the point (x₁, y₁) on the circle x² + y² + 2gx + 2fy + c= 0.

We take a neighboring point Q (x₂, y₂) on the circle as shown in the figure.

As P and Q lie on the circle, we have
x₁² + y₁² + 2gx₁ + 2fy₁ + c= 0 …………(i)
and x₂² + y₂² + 2gx₂ + 2fy₂ + c= 0 …………(ii)

∴ Subtracting (i) from (ii), we get
(x₂² – x₁²) + (y₂² – y₁²) + 2g (x₂ – x₁) + 2f (y₂ – y₁) = 0
⇒ (x₂ – x₁) (x₁ + x₂) + (y₂ – y₁) (y₁ + y₂) + 2g (x₂ – x₁) + 2f (y₂ – y₁) = 0
⇒ (y₂ – y₁) / (x₂ – x₁) = – (x₁ + x₂ + 2g) / (y₁ + y₂ + 2f) …………(iii)

Now, equation to PQ is
y – y₁ = [ (y₂ – y₁) / (x₂ – x₁) ] (x – x₁)
⇒ y – y₁ = [ – (x₁ + x₂ + 2g) / (y₁ + y₂ + 2f) ] (x – x₁) from (iii)

As Q → P, x₂ → x₂ and y₂ → y₁ and PQ become tangent to the circle at P. The equation of the tangent then becomes.

y – y₁ = [ – { 2 (x₁ + g) } / { 2 (y₁ + f) } ] (x – x₁)
⇒ (y – y₁) (y₁ + f) = – (x – x₁) (x₁ + g)
⇒ yy₁ + fy – y₁² – fy₁ = – (xx₁ + gx – x₁² – gx₁)
⇒ xx₁ + yy₁ + gx + fy = x₁² + y₁² + gx₁ + fy₁

Adding (gx₁ + fy₁ + c) on both sides, we get
xx₁ + yy₁ + g (x + x₁) + f (y + y₁) + c = x₁² + y₁² + 2gx₁ + 2fy₁ + c = 0

Thus, the equation of the tangent to the circle x² + y² + 2gx + 2fy + c = 0 at (x₁, y₁) is
xx₁ + yy₁ + g (x + x₁) + f (y + y₁) + c = 0

Note: The equation of the tangent to a curve at a point (x₁, y₁) may be obtained from the equation of the curve replacing x² by xx₁, y² by yy₁, x by (1/2) (x + x₁), y by (1/2) (y + y₁) and retaining the constant terms.

Length of the Tangent from an External Point:

Length of the Tangent from an Externa Point

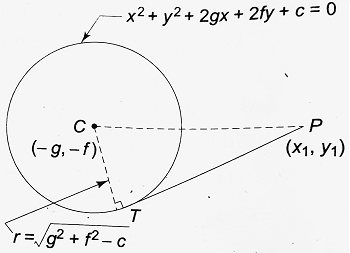
Let x² + y² + 2gx + 2fy + c = 0 be a circle and let P (x₁, y₁) be a point lying outside the circle. PT is tangent to the circle through P. Obviously, CT is the radius of the circle, and ∠CTP = 90°. The coordinates of C are (-g, -f) as shown in the figure.

In the right triangle CTP,
CP² = PT² + CT²
∴ PT² = CP² – CT²

⇒ PT² = (x₁ + g)² + (y₁ + f)² – [ √(g² + f² – c) ]²
⇒ PT² = x₁² + 2gx₁ + g² + y₁² + 2fy₁ + f² – g² – f² + c = 0
⇒ PT² = x₁² + y₁² + 2gx₁ + 2fy₁ + c
∴ PT =√( x₁² + y₁² + 2gx₁ + 2fy₁ + c)

Note: If S = 0 be a circle. Then, the length of the tangent drawn from an external point (x₁, y₁) is given by √S₁, where S₁ is the value of S obtained by putting x = x₁, y = y₁.

PT² = x₁² + y₁² + 2gx₁ + 2fy₁ + c

The square of the length of the tangent drawn from an external point P (x₁, y₁) is called the power of point P with respect to the circle under consideration.

Example 1: Find the equation of tangent to the circle x² + y² – 2x – 10y + 1 = 0 at (-3, -2).

Solution- Equation of a tangent to the circle x² + y² – 2x – 10y + 1 = 0 at (-3, -2) is-

x (-3) + y (-2) – 2 [ {x + (-3)} / 2 ] – 10 [ {y + (-2)} / 2 ] + 1 = 0
⇒ -3x – 2y – x + 3 – 5y + 10 + 1 = 0
⇒ -4x – 7y + 14 = 0
⇒ 4x + 7y – 14 = 0

Example 2: Find the equations of tangents to the circle x² + y² – 6x + 4y – 12 = 0 which are parallel to the line 4x + 3y + 5 = 0.

Solution- Let the equation of tangent parallel to the line 4x + 3y + 5 = 0 be

4x + 3y + k = 0 ………..(i)

Now, the equation of a circle is-
x²+ y² – 6x + 4y – 12 = 0

Here, the center (3, -2)
and radius (r) = √[3² + 2²– (-12) ]
⇒ r = √(13 + 12) = √25 = 5

Since the line (i) is tangent to the circle, therefore the distance of the line (i) from the center (3, -2) of the circle is equal to the radius of the circle.

⇒ | 4(3) + 3(-2) + k | / √[ (4)² + (3)²] = 5
⇒ | 6 + k | / 5 = 5
⇒ | 6 + k | = 25
⇒ 6 + k = ± 25
⇒ 6 + k = 25 or 6 + k = -25
⇒ k = 19 or k = -31

∴ The required equation of tangent is,
4x + 3y + 19 = 0 and 4x + 3y – 31 = 0

Example 3- The line 4x – 3y + 12 = 0 is a tangent at (-3, 0), and the line 3x + 4y = 16 is a tangent at (4, 1) to the circle. Find the equation of the circle.

Solution- The equation of the tangent at (-3, 0) to the circle is,
4x – 3y + 12 = 0

∴ The equation of Normal at (-3, 0) is-
3x + 4y + k = 0 ……….(i)

Now (i) passes through (-3, 0)
∴ 3(-3) + 4(0) + k = 0
⇒ k = 9

Equation (i) becomes-
3x + 4y + 9 = 0 ……….(a)

Now equation of the tangent at (4, 1) to the circle is,
3x + 4y – 16 = 0

∴ The equation of Normal at (4, 1) is-
4x – 3y + λ = 0 ……….(ii)

Now (ii) passes through (4, 1)
∴ 4(4) – 3(1) + λ = 0
⇒ 16 – 3 + λ = 0
⇒ λ = -13

Equation (ii) becomes-
4x – 3y -13 = 0 ……….(b)

Equations (a) and (b) represent the equation of the diameter of a circle which one solving gives the center of the circle.

Solving (a) and (b),

x / (-52 + 27) = y / (36 + 39) = 1 / (-9 – 16)
⇒ x/-25 = y/75 = 1/-25
⇒ x = 1, y = -3

∴ Coordinates of the center of the circle are (1, -3)

Now, Radius = Distance between points (1, -3) and (-3, 0)
⇒ r = √ [ (-3 -1)² + (0 + 3)²
⇒ r = √(16 + 9) = √25 = 5

Thus, the equation of the circle is,
(x – 1)² + [y – (-3)]² = (5)²
⇒ x² + 1 – 2x + y² + 9 + 6y = 25
⇒ x² + y² – 2x + 6y – 15 = 0