Concept of Binding Energy

Binding Energy:

Protons and Neutrons are bound together in the nucleus with the help of Nuclear force. A definite amount of work has to be done to separate the protons and neutrons to such a distance that they may not interact with each other again. This work done is the measure of the Binding Energy of the nucleus.

Thus, Binding Energy is defined as the energy with which the nucleons are bound in the nucleus. It is measured by the work required to be done to separate the protons and neutrons to such a distance that they may not interact again with each other.

Mass Defect:

It is found that the rest mass of the nucleus is always less than the sum of the rest masses of free protons and neutrons. This difference between the sum of masses of protons and neutrons forming the nucleus and the mass of the nucleus is called the mass defect.

Expression for Binding Energy:

In the nucleus _ZX^A,

Z = Atomic Number

A = Mass Number

m_p = Mass of Proton

m_n = Mass of Neutron

m_N = Mass of Nucleus of _ZX^A

Mass Defect, Δm = [Zm_p + (A-Z)m_n – m_N]

From Einstein’s mass Energy Equivalence,

B.E. = [Zm_p + (A-Z)m_n – m_N]C² ……….(1)

Where ‘C’ is the velocity of light in a Vacuum.

Add and subtract Zm_e in Equation (1), we have-

B.E. = [Zm_p + Zm_e + (A-Z)m_n – m_N – Zm_e]C²

B.E. = [Z(m_p + m_e) + (A-Z)m_n – (m_N + Zm_e)]C²

But (m_p + m_e) = m_H = mass of Hydrogen Nucleus

and (m_N + Zm_e) = m(_ZX^A) = mass of nucleus _ZX^A

B.E. = [Zm_H + (A-Z)m_n – m(_ZX^A)]C² …………….(2)

It is the required expression for B.E.

Average B.E./nucleon is defined as the total B.E. divided by a mass number of the nucleus. The variation of Average B.E./Nucleon with mass number is shown in the figure.

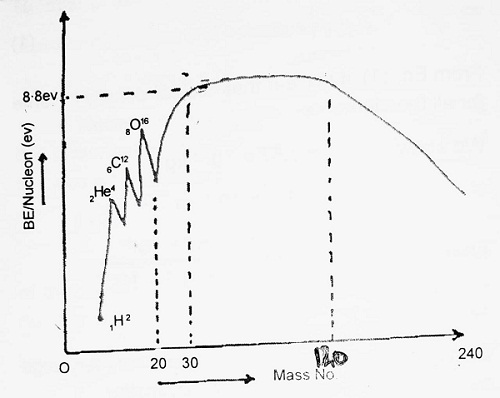
From the graph, we note that-

• Average B.E./Nucleon for light nuclei like ₁H¹, ₁H² etc. is small.
• From mass number 2 to mass number 20, there are various peaks for ₂He⁴, ₆C¹² and ₈O¹⁶. These peaks show that these nuclei are more stable than neighbouring nuclei.
• B.E. curve remains almost flat from mass number 30 to mass number 120. The B.E./Nucleon in this region is almost constant ≃ 8.8 Mev.
• From mass number 120 to mass number 240, BE/Nucleon decreases sharply, this shows that heavier nuclie are also less stable.

Importance of B.E. Curve:

(I) From the B.E. curve, we note that heavier nuclei are less stable. Hence, energy can be released in the nuclear fission of a single heavy nucleus. This is the basis of nuclear fission.

(II) From the B.E. curve, we also note that lighter nuclei like Hydrogen are also less stable. Hence energy can also be released, when we combine two lighter nuclei to form a single middle mass nucleus. This is the basis of nuclear fusion.