Table of Contents
Definite and Indefinite Integral:
Definite and indefinite integrals are the two main and well-known types of integrals. The integral is a subtype of calculus that is used to calculate the area under the curve with respect to the corresponding variable.
This topic is rather difficult that students find tough while solving its problems. The rules of integration play a vital role in calculating the problems of integral. In this lesson, we will discuss the definition, formulas, and examples of the definite and indefinite integral.
What are the Definite and Indefinite Integrals?
Before going to explain the definite and indefinite integral, let us discuss the subtype of calculus that is integral. The term that is used to calculate the area under the curve is known as integral calculus. It is a well-known branch of calculus that deals with the theory and applications of integrals.
The main purpose of this type of calculus is to calculate the new function or the numerical value of the function. It reverses the process that a derivative does. The limit calculus is also used to define this subtype of calculus.
Definite Integral:
The type of integration that is used to calculate the numerical value of the function with the help of the upper and lower limit value is known as the definite integral. The boundary values are applied to the function after integrating it.
The fundamental theorem of calculus is a helpful way to apply the upper and lower limit value to the integrated function. According to this theorem, the upper limit is applied to the integrated function first and then the lower limit with a minus sign between them.
The general expression of this subtype of the definite integral is:
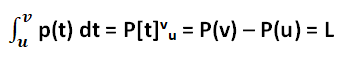
Indefinite Integral:
The type of integration that is used to calculate the new function whose original function is derivative (rate of change) is known as the indefinite integral. The boundary values are not applied to the function after integrating it.
The upper and lower limit values are not used in this subtype of integral. The constant of integration must be written in the indefinite integral after integrating the function. The general expression of this subtype of the indefinite integral is:
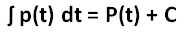
How do calculate the problems of Definite and Indefinite integral?
The problems of the definite and indefinite integral can be solved easily with the help of the rules of integration. Let us take a few examples of the definite and indefinite integral to learn how to calculate them.
| Example 1: For the indefinite integral Integrate the function with respect to “t” by using the indefinite type of integral. p(t) = 12t3 + 24t5 – 4t7 + 12sin(t) + 10t – 12 Solution: Step 1: First of all, take the given function and integrating variable and write it according to the general expression of the indefinite integral. p(t) = 12t3 + 24t5 – 4t7 + 12sin(t) + 10t – 12 integrating variable = t ʃ p(t) dt = ʃ [12t3 + 24t5 – 4t7 + 12sin(t) + 10t – 12] dt Step 2: Now take the above function and apply the sum and difference laws of integration and write the notation of integral to each term separately and take out the constant coefficients outside the integral notation. ʃ [12t3 + 24t5 – 4t7 + 12sin(t) + 10t – 12] dt = ʃ [12t3] dt+ ʃ [24t5] dt – ʃ [4t7] dt + ʃ [12sin(t)] dt + ʃ [10t] dt – ʃ [12] dt ʃ [12t3 + 24t5 – 4t7 + 12sin(t) + 10t – 12] dt = 12ʃ [t3] dt+ 24ʃ [t5] dt – 4ʃ [t7] dt + 12ʃ [sin(t)] dt + 10ʃ [t] dt – ʃ [12] dt Step 3: Now integrate the above expression with the help of power and trigonometry laws of integration. = 12 [t3+1 / 3 + 1]+ 24 [t5+1 / 5 + 1] – 4ʃ [t7+1 / 7 + 1] + 12 [-cos(t)] + 10 [t1+1 / 1 + 1] – [12t] + C = 12 [t4 / 4]+ 24 [t6 / 6] – 4 [t8 / 8] + 12 [-cos(t)] + 10 [t2 / 2] – [12t] + C = 12/4 [t4]+ 24/6 [t6] – 4/8 [t8] + 12 [-cos(t)] + 10/2 [t2] – [12t] + C = 3 [t4]+ 4 [t6] – 1/2 [t8] + 12 [-cos(t)] + 5 [t2] – [12t] + C = 3 [t4]+ 4 [t6] – 1/2 [t8] – 12 [cos(t)] + 5 [t2] – [12t] + C = 3t4 + 4t6 – t8 /2- 12cos(t) + 5t2 – 12t + C = 3t4 + 4t6 – 0.5t8– 12cos(t) + 5t2 – 12t + C The above problem of the indefinite integral can also be solved by using an integral calculator to avoid such a large number of steps in calculating the new function.  |
| Example 2: For the indefinite integral Integrate the function with respect to “t” by using the indefinite type of integral. p(t) = 12t+ 24t3 – 14t6 + 10t2 – 102 in the interval of [1, 5] Solution: Step 1: First of all, take the given function and integrating variable and write it according to the general expression of the definite integral. p(t) = 12t+ 24t3 – 14t6 + 10t2 – 102 integrating variable = t 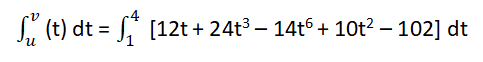 Step 2: Now take the above function and apply the sum and difference laws of integration and write the notation of integral to each term separately and take out the constant coefficients outside the integral notation. 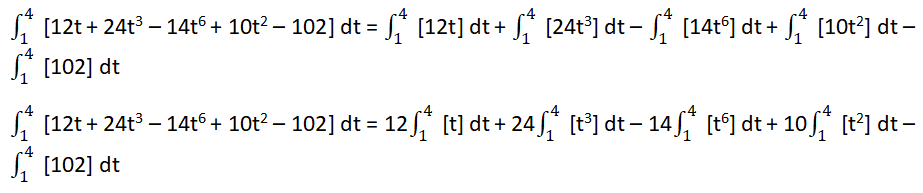 Step 3: Now integrate the above expression with the help of the power law of integration. = 12 [t1+1/ 1 + 1]41+ 24 [t3+1/ 3 + 1]41 – 14 [t6+1/ 6 + 1]41+ 10 [t2+1/ 2 + 1]41 – [102t]41 = 12 [t2/ 2]41+ 24 [t4/ 4]41 – 14 [t7/ 7]41+ 10 [t3/ 3]41 – 102 [t]41 = 12/2 [t2]41+ 24/4 [t4]41 – 14/7 [t7]41+ 10/3 [t3]41 – 102 [t]41 = 6 [t2]41+ 6 [t4]41 – 2 [t7]41+ 10/3 [t3]41 – 102 [t]41 Step 4: Now use the fundamental theorem of calculus to apply the upper and lower limit values to the above-integrated value. = 6 [42 – 12]+ 6 [44 – 14]– 2 [47 – 17]+ 10/3 [43 – 13] – 102 [4 – 1] = 6 [16 – 1]+ 6 [256 – 1]– 2 [16384 – 1]+ 10/3 [64 – 1] – 102 [4 – 1] = 6 [15]+ 6 [255]– 2 [16383]+ 10/3 [63] – 102 [3] = 90+ 1530– 32766+ 630/3 – 306 = 90+ 1530– 32766+ 210 – 306 = 1620– 32766+ 210 – 306 = -31146+ 210 – 306 = -30936 – 306 = -31242 |
Final words:
In this lesson, we have learned all the basics of the definite and indefinite integral. We have covered all the basic intent of the targeted keyword. Now you are able to solve any problem of the definite and indefinite integral just by following the above formulas and solved examples.









Comments (No)