Table of Contents
Moment of a Force and Couple:
Moment of a Force:
A body is said to be perfectly rigid if the distance between any two particles in it remains constant. It does not suffer any change in its shape on the application of force. Since all the bodies yield more or less to the action of forces, nobody is, therefore, perfectly rigid. The effect of a force on a rigid body depends on the magnitude of the force and its line of action (the straight line along which the force acts). The force acting on a rigid body may produce a rotatory motion or a translator motion. The tendency of a force to produce rotation in a body about a given axis is known as the moment of a force. It is also called torque.
Let us consider a rigid body with a fixed axis M, within it. Suppose that a force ‘F’ is applied to it. Now the turning effect of force ‘F’ depends on its magnitude and the line in which the force acts. Thus, the moment of the force about the point ‘M’ is given by the quantity F X MN.
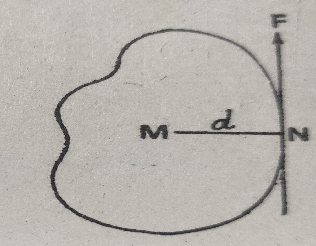
Hence, the moment of a force or torque (T) is measured by the product of the force applied and the perpendicular distance from the axis of rotation to the line of action of the force called the moment arm.
Therefore, T = Force X Moment Arm = F X MN = F x d
When no force is applied (i.e., F = 0) or when the line of action of force passes through the axis of rotation (i.e., d = 0), the moment of the force or torque (the rotating effect of force) will be equal to zero.
The moment of force is termed 1 C.G.S. unit of moment if a body is acted upon by a force of 1 dyne at a distance of 1 cm from its axis of rotation and it is called 1 F.P.S. unit of moment if a body is acted upon by a force of 1 poundal at a distance of 1 foot from its axis of rotation.
When on applying a force, the body rotates in a clockwise direction the moment is said to be negative or clockwise moment and if, on the other hand, the applied force produces rotation in a body in the anticlockwise direction the moment is said to be positive or anticlockwise moment.
Principle of Moments:
When a number of forces acting on a body in the same plane keep it in equilibrium, the sum of clockwise moments about any point is equal to the sum of anti-clockwise moments. This is known as the principle of moments.
Parallel Forces:
The forces acting on a rigid body are said to be parallel when their lines of action are parallel to each other. For example- when a tonga is pulled by two horses, it is acted upon by two parallel forces in the same direction.
Parallel Forces may be-
- Like Parallel Forces- When the forces act in the same direction.
- Unlike Parallel Forces- When the forces act in the opposite direction.
The resultant (R) of like parallel forces (P and Q) is equal to their sum and the resultant of unlike parallel forces is equal to their difference. Thus,
In case of like parallel forces, R = P + Q
In case of unlike parallel forces, R = P- Q
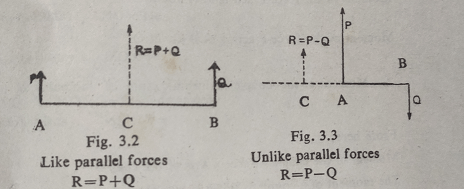
The direction of resultant of like parallel forces is the same as that of component forces. While on the other hand, the direction of resultant of unlike parallel forces is parallel to the direction of the greater component. The resultant of like parallel forces divide the distance between the forces internally in the inverse ratio of the component forces (thus in the fig. P X AC = Q X BC) and the resultant of two, unlike parallel forces, does so externally in the inverse ratio of the component forces (Thus in the fig. P X AC = Q X BC).
Couple:
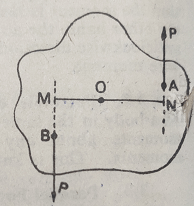
A couple is a pair of two equal and unlike parallel forces acting at different points of a body. Thus, if two forces ‘P’ and ‘P’ of the same magnitude act on a rigid body in opposite directions at points A and B, they constitute a couple. The resultant of the couple being zero (P – P = 0), the couple does not produce any translatory motion. The effect of a couple on a body is, therefore, only to produce rotatory motion in it.
Winding a clock, opening a lock with a key and opening or closing a water tap are the common examples of a couple.
The turning effect of a couple is known as the moment of the couple. It is equal to the product of either of the forces and the perpendicular distance between the lines of action of the two forces. The perpendicular distance between the lines of action of the forces of a couple is referred to as the arm of the couple. The moment of a couple is also known as torque.
Let ‘O’ be the point about which the moment is to be taken and OM and ON be its perpendicular distances from the lines of action of the two forces P and P.
Now, Moment of the force P acting at A about O = P X ON (anticlockwise)
Moment of the force P acting at B about O = P X OM (anticlockwise)
Therefore, Moment of the couple = Algebraic sum of moments of two forces about O = P X ON + P X OM = P X MN (anticlockwise)
From here,
Moment of the couple = Force X Arm of the couple
The moment of a couple is taken as positive if the couple tends to turn a body in the anticlockwise direction and negative if in the opposite direction i.e. clockwise direction. It is, therefore, a vector quantity.
The moment of a couple is expressed as dyne-cm or gm-cm in C.G.S system and newton-metre or kg-metre in M.K.S system.









Comments (No)