Rotational Quantities as Vectors

Rotational Quantities as Vectors:

A quantity that can be completely described by its magnitude and direction is not necessarily a vector quantity. There is another requirement that must be fulfilled before it is called a vector quantity. The additional requirement is regarding addition. If the quantity under discussion has a magnitude and a direction and is added according to the well-known operation of vector addition then and only then it is called a vector quantity. The law of vector addition shows that it makes no difference in what order we add vectors i.e., the commutative law, A + B = B + A, is obeyed by the vectors.

Let us consider the angular displacement θ, of a rigid body that is capable of rotation about a fixed axis. The angular displacement has a magnitude (the angle of rotation) as well as a direction (the direction of the axis following the right-hand screw rule). However, angular displacements are not vectors because they do not add like vectors. It can be seen that the sum of two angular displacements is not commutative, i.e.,

θ₁ + θ₂ ≠ θ₂ + θ₁

This can be verified easily by giving two rotations as described below to a book. Suppose a book is initially oriented as shown in figure (a) with its letters FRONT towards the observer. The book is first rotated through 90° about XX’ and then about ZZ’ axis, the final orientation being as shown in figure (c). Now we again start with the initial orientation as shown in figure (a). Suppose we first rotate the book through 90° about ZZ’ and then about XX’ axis. The final orientation of the book is shown in figure (e). Since the final orientation in two cases (c) and (e) are not the same, we conclude that the commutative law of vector addition is not obeyed by angular displacement. Hence finite angular displacements are not vector quantities.

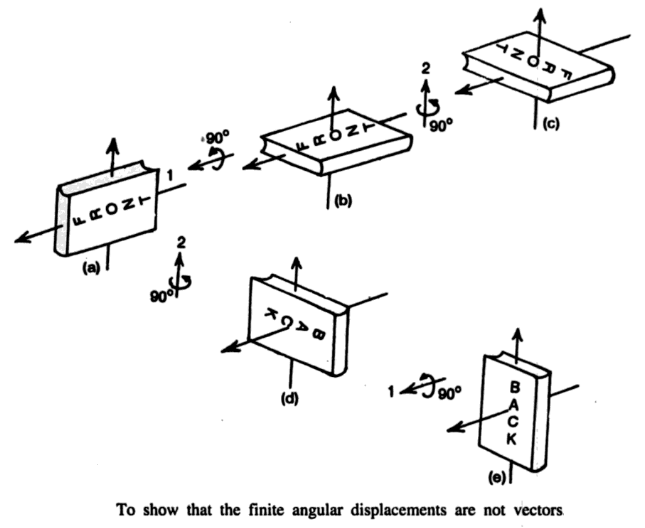
If, however, the same operations are repeated but with small rotations, say 2° – 3° (instead of 90°) we shall see that the final orientations in the two cases would still be different but the difference would be much smaller. As the two rotations are made still smaller, the difference between the final orientations in the two cases would further decrease. If the rotations are made infinitesimal, the order of addition no longer affects the final results. Hence infinitesimally small angular displacements are vector quantities.

Quantities that are defined in terms of infinitesimally small displacements would also be vectors. One of such quantities is angular velocity ω (= dθ/dt). The angular velocity is, therefore, a vector quantity. It is represented by an arrow drawn along the axis of rotation, the length of the arrow is proportional to the magnitude of angular velocity, and its direction is according to the right-hand rule (i.e. if we curl the fingers of the right hand around the axis of rotation so that fingers point in the direction of rotation then the thumb will point in the direction of angular velocity vector.