Table of Contents
Slope of a Line:
The inclination of a line to the X-axis ranges from 0° to 180°. By the term inclination, we refer to the angle that the line makes with the positive direction of the X-axis.

The slope or the gradient of a line is the tangent of the angle that the line makes with the positive direction of the X-axis. Thus, if θ is the inclination of the line, then its slope is given by m = tan θ as shown above.
| If θ = 0, then m = 0 If 0 < θ < π/2, then m > 0 If π/2 < θ < π, then m < 0 If θ = π/2, then 1/m = cot θ = 0 |
If a non-vertical line passes through two distinct points (x1, y1) and (x2, y2), then the slope of the line is given by, m = (y2 – y1)/(x2 – x1) = (y1 – y2)/(x1 – x2).

| In figure (b), when 0 < θ < π/2 slope m = tan θ ⇒ slope m = QN/PN = (y2 – y1)/(x2 – x1) ⇒ slope m = (y1 – y2)/(x1 – x2) |
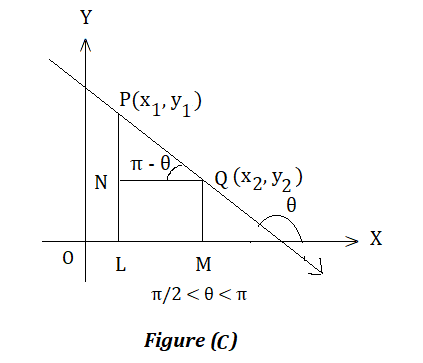
| In figure (c), when π/2 < θ < π slope m = tan θ ⇒ slope m = – tan (π – θ) ⇒ slope m = – PN/NQ ⇒ slope m = – (y1 – y2)/(x2 – x1) = (y2 – y1)/(x2 – x1) ⇒ slope m = (y1 – y2)/(x1 – x2) |

| Note: (i) If θ = 0, then slope m = (y2 – y1)/(x2 – x1) = 0/PQ = 0 as shown in figure (d). (ii) If θ = π/2, then tan θ is undefiend. In such a case, when the line is vertical, for the sake of mathematical calculation, we take 1/m = 0. |
Parallel and Perpendicular Lines:
(1) Parallel Lines- Two parallel lines have the same slope.

We consider two parallel lines l1 and l2 having slopes m1 and m2 (none of them being parallel to the Y-axis) respectively and let the lines make angles α1 and α2 respectively with the positive direction of the X-axis. Thus, m1 = tan α1 and m2 = tan α2.
| Since the lines are parallel to each other, α1 = α2 ∴ tan α1 = tan α2 i.e. m1 = m2 Thus, two parallel lines will always have the same slope. |
Two lines having the same slope are parallel to each other.
We now consider two lines l1 and l2 having the same slope.
∴ m1 = m2, i.e., tan α1 = tan α2 ⇒ α1 = α2
Thus, the lines l1 and l2 are parallel to each other.
Conclusion: If two lines are parallel then they will have the same slope and conversely, if two lines have the same slope then they will be parallel to each other.
(2) Perpendicular Lines- The product of the slope of two perpendicular lines is -1.
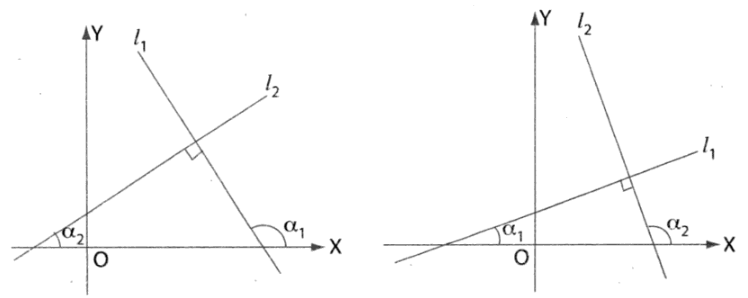
We consider two perpendicular lines l1 and l2 having slopes m1 and m2. Let α1 and α2 respectively be the angles made by them with the positive direction of the X-axis.
Thus, either α1 = 90° + α2 or, α2 = 90° + α1
| Case 1: α1 = 90° + α2 ∴ tan α1 = tan (90° + α2) or, tan α1 = – cot α2 or, tan α1 = – 1/tan α2 or, m1 = -1/m2 or, m1m2 = -1 Case 2: α2 = 90° + α1 ∴ tan α2 = tan (90° + α1) or, tan α2 = – cot α1 or, tan α2 = – 1/tan α1 or, m2 = -1/m1 or, m1m2 = -1 Thus, the product of the slopes of two perpendicular lines is -1. |
If the product of the slopes of two lines is -1, then they are perpendicular to each other.
| Let m1m2 = -1 ∴ m1 = -1/m2 or, tan α1 = -1/tan α2 = -cot α2 = tan (90° + α2) ∴ Either α1 = 90° + α2 or, 180° + α1 = 90° + α2 i.e., Either α1 – α2 = 90° or, α2 – α1 = 90° In both cases, the lines are perpendicular to each other. |
Conclusion: If two lines are perpendicular, then the product of their slopes is -1 and conversely if the product of the slope of two lines is -1, then they are perpendicular to each other.
Thus, if the slope of a line is m1 (≠ 0), then the slope of any line perpendicular to it will be -1/m1.
Observation: If a line has a slope of 2/3, then any line parallel to it will have a slope of 2/3, and any line perpendicular to it will have a slope of -3/2 [∵ 2/3 x (-3/2) = -1].
Intercepts of a line on the coordinate axes:
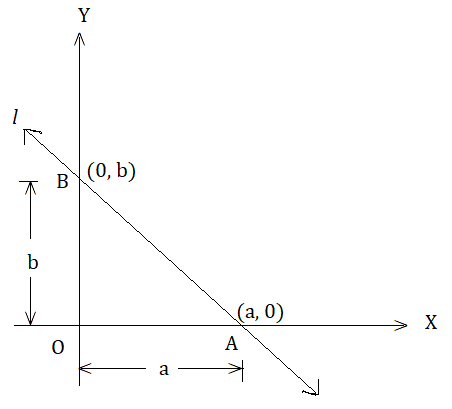
If a line l intersects the X-axis at A and the Y-axis at B, then for A, y = 0, and for the point B, we must have x = 0. If a and b are the intercepts of the line on the X and Y-axes then the coordinates of A and B are (a, 0) and (0, b) respectively.









Comments (No)