Table of Contents
Define Circle:
A circle is the locus of a point that moves in a plane so that its distance from a fixed point, called the centre, is always constant. The constant distance is called the radius of the circle.
Equation to a Circle when the centre is at the Origin:
Let the centre of the circle be O and let r be its radius. Let P be any point on the circle whose coordinates are (x, y) in reference to the rectangular axes OX and OY as shown in the figure.
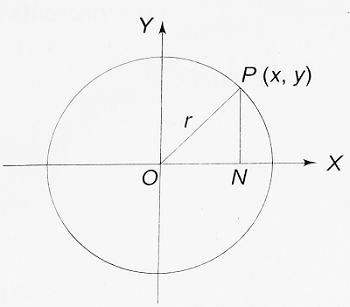
PN is drawn perpendicular to OX. O and P are joined. OP = r. In right △PON,
| ON2 + PN2 = OP2 ⇒ x2 + y2 = r2 ……….(i) |
This being the relation that holds good between the coordinates of any point on the circle, is the required equation.
The above form shows that the equation is of second degree in which the coefficients of x2 and y2 are equal and in which there is no term containing xy.
Equation to a Circle whose centre is at (α, β):
Let C be the centre of the circle whose coordinates are (α, β) in reference to the rectangular axes OX and OY.
Let P(x, y) be any point on the circle. CL and PM are drawn perpendicular to OX. C and P are joined. Then, CP = r. CN is drawn perpendicular to PM as shown in the figure.

| In the right △PCN, CN2 + PN2 = CP2 ∴ (OM – OL)2 + (PM – NM)2 = CP2 ∴ (OM – OL)2 + (PM – CL)2 = r2 ⇒ (x – α)2 + (y – β)2 = r2 ……….(ii) which is the required equation. |
Notes:
| (i) If the centre be the origin, then α = 0, β = 0. Equation (ii) then reduces to x2 + y2 = r2. (ii) On further simplification, equation (ii) becomes x2 + y2 – 2αx – 2βy + (α2 + β2 – r2) = 0 or, x2 + y2 + 2gx + 2fy + c = 0, where α = -g, β = -f and c = α2 + β2 – r2 Thus, the equation x2 + y2 + 2gx + 2fy + c = 0 ……….(iii) always represents a circle whose centre is (-g, -f) and whose radius is given by r = √(g2 + f2 – c) [∵ c = α2 + β2 – r2, r2 = α2 + β2 – c = (-g)2 + (-f)2 – c = g2 + f2 – c] If g2 + f2 ≥ c, the circle is real. However, g2 + f2 = c implies that the radius of the circle is 0, that is, the circle then becomes a point circle. If g2 + f2 < c, the circle becomes imaginary. It is now obvious that the general equation in second degree, i.e., ax2 + 2hxy + by2 +2gx + 2fy + c = 0 represents a circle if a = b and h = 0. Equation (iii) is known as the general form of the equation to a circle. To find its centre and radius we rewrite the equation as x2 + 2gx + y2 + 2fy + c = 0 ⇒ (x2 + 2gx + g2) + (y2 + 2fy + f2) = g2 + f2 – c ⇒ (x + g)2 + (y + f)2 = [√(g2 + f2 – c)]2 Which is comparable to (x – α)2 + (y – β)2 = r2. Thus, the centre of the circle is (-g, -f) and its radius = √(g2 + f2 – c) To get the centre and radius of the circle directly from its equation, we write the equation in the general form (where the coefficient of x2 and y2 are both 1). Then the coordinates of the centre are (-1/2 coefficient of x, -1/2 coefficient of y). 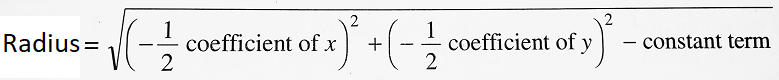 |
Equation to the Circle described on the line segment joining the points (x1, y1) and (x2, y2) as diameter:
Let A be the point (x1, y1) and B, the point (x2, y2) and let the coordinates of any point P on the circle be (x, y). AP, BP, and AB are drawn as shown in the figure.
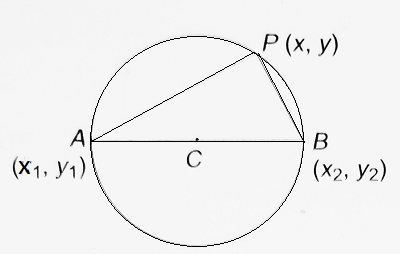
| The slope of AP is (y – y1)/(x – x1) = m1 and that of BP is (y – y2)/(x – x2) = m2 Now, ∠APB = π/2 as AB is a diameter ∴ m1m2 = -1 ⇒ [(y – y1)/(x – x1)] [(y – y2)/(x – x2)] = -1 ⇒ (x – x1) (x – x2) = – (y – y1) (y – y2) Thus, (x – x1) (x – x2) + (y – y1) (y – y2) = 0 is the required equation to the circle.  |
Position of a point with respect to a Circle:
Let us consider the circle x2 + y2 + 2gx + 2fy + c = 0 whose centre C is at (-g, -f) and whose radius = √(g2 + f2 – c).
Now let P (x1, y1) be a point. Then, CP = √[(x1 + g)2 + (y1 + f)2]
The point P lies outside, on, or inside the circle according as CP >, = OR < CR, where CR is the radius of the circle as shown in the figure.

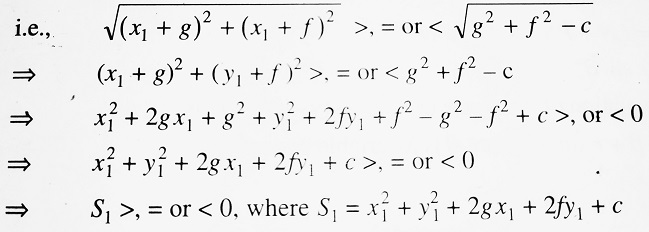
Equation to a Circle in the Parametric Form:
Case (i) When the centre is at the origin:
Let P(x, y) be any point on the circle x2 + y2 = a2, and let OP make an angle θ with the positive direction of the X-axis. Then, ∠PON = θ as shown in the figure.
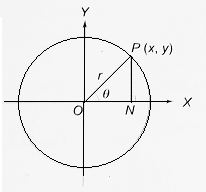
| ∴ x = ON = r cos θ y = PN = r sin θ Thus, the parametric form of the circle whose centre is as the origin and whose radius is r is given by x = r cos θ, y = r sin θ |
Case (ii) When the centre is at the point (α, β):
Let P(x, y) be any point on the circle (x – α)2 + (y – β)2 = r2. CM and PL are drawn perpendicular on OX and CN is drawn perpendicular to PL as shown in the figure.
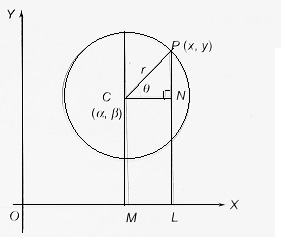
| In the right triangle PCN, ∠PCN = θ, CP = r In the right triangle PCN, CN = CP cos θ = r cos θ and PN = CP sin θ = r sin θ ∴ x = OL = OM + ML = OM + CN = α + r cos θ and y = PL = LN + PN = CM + PN = β + r sin θ Thus, the parametric equation of the circle (x – α)2 + (y – β)2 = r2 is x = α + r cos θ, y = β + r sin θ, where θ is a variable parameter. |








Comments (No)