Profit and Loss:
Profit and loss are the terms related to transactions in trade and business. Whenever a purchased article is sold, then either profit is earned or loss is incurred.
(a) Cost Price (CP)- The price at which an article is purchased, is called its cost price.
(b) Selling Price (SP)- The price at which an article is sold, is called its selling price.
(c) Profit (SP > CP)- If the selling price of an article is more than its cost price, then there is a gain or profit.
| Profit = Selling Price – Cost Price or Profit = SP – CP |
(d) Loss (SP < CP)- If the selling price of an article is less than its cost price, then there is a loss.
| Loss = Cost Price – Selling Price or Loss = CP – SP |
(e) Profit and Loss formula:

| Note: Profit % or Loss % is always calculated on CP. |

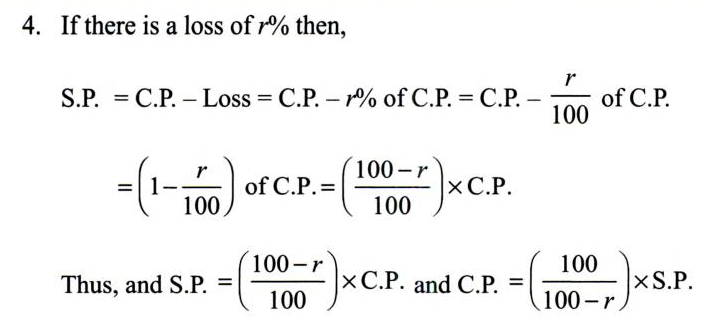
(e) Overhead Expenses- Sometimes apart from paying the cost of an article, a person has to spend money on its transportation (cartage), labor charges, repair, sales tax, etc. Such expenses are known as overhead expenses.
Overhead Expenses are always included in the cost price of the article. Thus, we have-
| Actual CP of the article = Cost of the article + Overhead Expenses |
Profit and Loss Examples:
| Example 1: Andrew purchased a bike for $6 lac and sold it for $2 lac. Find profit/loss in this transaction. Solution- Here, SP < CP ∴ Loss is incurred in this case. According to the formula, Loss = CP – SP = $6 lac – $2 lac ∴ Loss = $4 lac |
| Example 2: Arnold buys a toy for $500 but because of certain urgency, he sells it for $300. Find his loss percentage. Solution- Given that CP = $500 SP = $300 Loss = CP – SP = $500 – $300 = $200 According to the formula, Loss % = (Loss/CP) x 100% ⇒ Loss % = (200/500) x 100% ⇒ Loss % = 40% |
| Example 3: John sells two wristwatches for $5865 each, gaining 15% on the one and losing 15% on the other. Find his gain or loss percentage on the whole transaction. Solution- For one wristwatch: SP = $5865, Gain% = 15% ∴ CP = [100/(100 + gain%)] x SP ⇒ CP = (100/115) x 5865 ⇒ CP = $5100 For the other wristwatch: SP = $5865, Loss% = 15% ∴ CP = [100/(100 – loss%)] x SP ⇒ CP = (100/85) x 5865 ⇒ CP = $6900 ∴ Total CP of the two wristwatches = 5100 + 6900 = $12000 Total SP of the two wristwatches = 5865 x 2 = $11730 ∴ Loss = CP – SP = 12000 – 11730 = $270 ∴ Loss % = (Loss/CP) x 100% ⇒ Loss % = (270/12000) x 100% ⇒ Loss % = (9/4)% |
| Example 4: A computer set was sold at a gain of 15%. Had it been sold for $575 more, the gain would have been 20%. Find the cost price of the set. Solution- Let the cost price of the computer set be $x. When the gain is 15%, then SP = x + 15% of x = $23x/20 When the gain is 20%, then SP = x + 20% of x = $6x/5 Now, the difference between the two SP’s = $575 ⇒ (6x/5) – (23x/20) = 575 ⇒ x/20 = 575 ⇒ x = 11500 ∴ The cost price of the set is $11500 |
| Example 5: A dealer buys a toy car for $450 and spends $30 on its repair. If he sells the toy car for $600, find his profit percent. Solution- Cost price of toy car = $450 Expenditure on repair = $30 ∴ Total cost of the toy car = $450 + $30 = $480 Now, we have SP = $600 ∴ Profit = SP – CP = 600 – 480 = $120 ∴ Profit % = (Profit/CP) x 100% ⇒ Profit % = (120/480) x 100% ⇒ Profit % = 25% |
| Example 6: A man sells a toy for $600 and incurs a loss equal to one-third of the selling price. Find his loss percentage. Solution- SP = $600 Loss = 1/3 of SP = 1/3 of $600 = $200 CP = SP + Loss = 600 + 200 = $800 ∴ Loss % = (Loss/CP) x 100% ⇒ Loss % = (200/800) x 100% ⇒ Loss % = 25% |
| Example 7: By selling 144 tables a shopkeeper suffered a loss equal to the SP of 6 tables. Find his loss percentage. Solution- Let the SP of one table be $x. SP of 144 tables = $144x SP of 6 tables = $6x ∴ Loss on selling 144 tables = $6x CP of 144 tables = SP + Loss = 144x + 6x = $150x ∴ Loss % = (Loss/CP) x 100% = (6x/150x) x 100% = 4% |
| Example 8: A shopkeeper mixes three varieties of wheat, $30, $25, and $35 per kg in a ratio of 3:4:2 in terms of weight. He sells the mixture at $33 per kg. Find his profit percentage. Solution- Suppose the shopkeeper bought 3kg, 4kg, and 2kg, respectively of the three varieties of wheat. Then, CP of 9kg wheat = (30 x 3 + 25 x 4 + 35 x 2) ⇒ CP of 9kg wheat = 90 + 100 + 70 = $260 SP of 9kg wheat = 33 x 9 = $297 Profit = 297 – 260 = $37 ∴ Profit % = (Profit/CP) x 100% ⇒ Profit % = (37/260) x 100% = (185/13)% |
| Example 9: A bought an article and spent $100 on its repair. He then sold it to B at a profit of 20%. After some time B sold it back to A at a loss of 20%. If A gains $240, what is the amount A spent on buying the article? Solution- Let the cost price for A be $z. He spent $100 on its repair. ∴ Total cost = $(z + 100), Gain = 20% ∴ SP = [(100 + 20)/100] x (z + 100) ⇒ SP = $(120/100) (z + 100) For B, CP = $(120/100) (z + 100) B’s loss = 20% of $(120/100) (z + 100) Now, A’s gain = B’s loss ⇒ $240 = 20% of $(120/100) (z + 100) ⇒ (20/100) (120/100) (x + 100) = 240 ⇒ (x + 100) = (240 x 100 x 100)/(20 x 120) ⇒ (x + 100) = 1000 ⇒ x = 900 Hence, A bought the article for $900. |









Comments (No)