Table of Contents
Trigonometry Formulas:
Trigonometric Ratios Formulas:
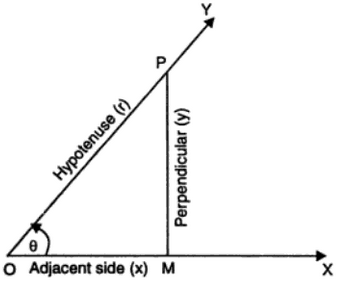
| sin θ = Perpendicular/Hypotenuse = MP/OP = y/r |
| cos θ = Adjacent Side or Base/Hypotenuse = OM/OP = x/r |
| tan θ = Perpendicular/Adjacent Side or Base = MP/OM = y/x |
| cosec θ = Hypotenuse/Perpendicular = OP/MP = r/y |
| sec θ = Hypotenuse/Adjacent Side or Base = OP/OM = r/x |
| cot θ = Adjacent Side or Base/Perpendicular = OM/MP =x/y |
Relation Between Trigonometric Ratios:
| sin θ = 1/cosec θ |
| cos θ = 1/sec θ |
| tan θ = sin θ/cos θ |
| cosec θ = 1/sin θ |
| sec θ = 1/cos θ |
| cot θ = cos θ/sin θ |
Trigonometric Identities:
| sin2 θ + cos2 θ = 1 |
| 1 + tan2 θ = sec2 θ |
| 1 + cot2 θ = cosec2 θ |
Trigonometry Table:
| Radian Measure = (π/180) x Degree Measure |
| Degree Measure = (180/π) x Radian Measure |
| Angles (In Radians) | 0 | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
| Angles (In Degrees) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| sin | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 |
| cos | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 |
| tan | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
| cot | ∞ | √3 | 1 | 1/√3 | 0 | ∞ | 0 | ∞ |
| sec | 1 | 2/√3 | √2 | 2 | ∞ | -1 | ∞ | 1 |
| cosec | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ |
Trigonometric Functions:
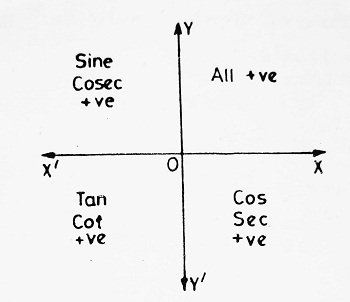
| I | II | III | IV | |
| sin θ | +ve | +ve | -ve | -ve |
| cos θ | +ve | -ve | -ve | +ve |
| tan θ | +ve | -ve | +ve | -ve |
| cosec θ | +ve | +ve | -ve | -ve |
| sec θ | +ve | -ve | -ve | +ve |
| cot θ | +ve | -ve | +ve | -ve |
| sin (π/2 – θ) = cos θ | sin (π/2 + θ) = cos θ |
| cos (π/2 – θ) = sin θ | cos (π/2 + θ) = – sin θ |
| tan (π/2 – θ) = cot θ | tan (π/2 + θ) = – cot θ |
| cot (π/2 – θ) = tan θ | cot (π/2 + θ) = – tan θ |
| sec (π/2 – θ) = cosec θ | sec (π/2 + θ) = – cosec θ |
| cosec (π/2 – θ) = sec θ | cosec (π/2 + θ) = sec θ |
| sin (π – θ) = sin θ | sin (π + θ) = – sin θ |
| cos (π – θ) = – cos θ | cos (π + θ) = – cos θ |
| tan (π – θ) = – tan θ | tan (π + θ) = tan θ |
| cot (π – θ) = – cot θ | cot (π + θ) = cot θ |
| sec (π – θ) = – sec θ | sec (π + θ) = – sec θ |
| cosec (π – θ) = cosec θ | cosec (π + θ) = – cosec θ |
| sin (-x) = – sin x | cos (-x) = cos x |
Addition and Subtraction Formulas in Trigonometry:
| sin (A + B) = sin A cos B + cos A sin B |
| sin (A – B) = sin A cos B – cos A sin B |
| cos (A + B) = cos A cos B – sin A sin B |
| cos (A – B) = cos A cos B + sin A sin B |
| tan (A + B) = (tan A + tan B)/(1 – tan A tan B) |
| tan (A – B) = (tan A – tan B)/(1 + tan A tan B) |
| cot (A + B) = (cot A cot B – 1)/(cot B + cot A) |
| cot (A – B) = (cot A cot B + 1)/(cot B – cot A) |
| sin (A + B). sin (A- B) = sin2 A – sin2 B |
| cos (A + B). cos (A- B) = cos2 A – sin2 B = cos2 B – sin2 A |
| sin (A + B + C) = cos A cos B cos C (tan A + tan B + tan C – tan A tan B tan C) |
| cos (A + B + C) = cos A cos B cos C (1- tan A tan B – tan B tan C – tan C tan A) |
| tan (A + B + C) = (tan A + tan B + tan C – tan A tan B tan C)/(1- tan A tan B – tan B tan C – tan C tan A) |
Sum and Difference of Sines or Cosines:
| 2 sin A cos B = sin (A + B) + sin (A – B) |
| 2 cos A sin B = sin (A + B) – sin (A – B) |
| 2 cos A cos B = cos (A + B) + cos (A – B) |
| 2 sin A sin B = cos (A- B) – cos (A + B) |
| sin C + sin D = 2 sin (C + D)/2 . cos (C – D)/2 |
| sin C – sin D = 2 cos (C + D)/2 . sin (C – D)/2 |
| cos C + cos D = 2 cos (C + D)/2 . cos (C – D)/2 |
| cos C – cos D = 2 sin (C + D)/2 . sin (D – C)/2 |
Trigonometrical Ratios of Multiple Angles:
| sin 2A = 2 sin A cos A = 2 tan A/(1 + tan2 A) |
| cos 2A = cos2 A – sin2 A = 2 cos2 A – 1 = 1 – 2 sin2 A = (1 – tan2 A)/(1 + tan2 A) |
| tan 2A = 2 tan A/(1 – tan2 A) |
| cot 2A = (cot2 A – 1)/2cot A |
| sin 3A = 3 sin A – 4 sin3 A |
| cos 3A = 4 cos3 A – 3 cos A |
| tan 3A = (3 tan A – tan3 A)/(1 – 3 tan2 A) |
Sine Formula:
| In any triangle ABC, a/sin A = b/sin B = c/sin C |
Cosine Formula:
| cos A = (b2 + c2 – a2)/2bc |
| cos B = (c2 + a2 – b2)/2ca |
| cos C = (a2 + b2 – c2)/2ab |
Projection Formula:
| a = b cos C + c cos B |
| b = c cos A + a cos C |
| c = a cos B + b cos A |









Comments (No)