Centre of Gravity:
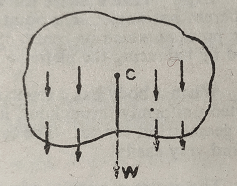
A body consists of a large number of small particles each of which is pulled down by a force, the force of gravity, towards the centre of the earth. Since the centre of the earth is at a very great distance from the body, the forces acting on a body may be considered as like parallel forces. These parallel forces have a resultant which acts in the direction of forces at the point C (the centre of parallel forces). The resultant of parallel forces acting on a body represents its weight (W) and the point at which it acts is called the centre of gravity (C.G.). Thus, the centre of gravity of a body is the fixed point in a body at which its whole mass may be supposed to act. It may also be defined as that point in a body through which the resultant of parallel forces acting on the various particles of a body passes, no matter in which position the body is put.
It should be noted that whether the body is at rest or in motion, the position of centre of gravity remains unaltered with respect to the body.
When a body is suspended from a point other than its centre of gravity, it comes to rest in such position that the centre of gavity lies vertically below the point of suspension. A plum line, the instrument used by masons to see that the wall remains vertical, is constructed on this principle. The plumb line consists of a heavy bob of lead (plumb bob) tied to a long thread.
Finding the Centre of Gravity of a Body:
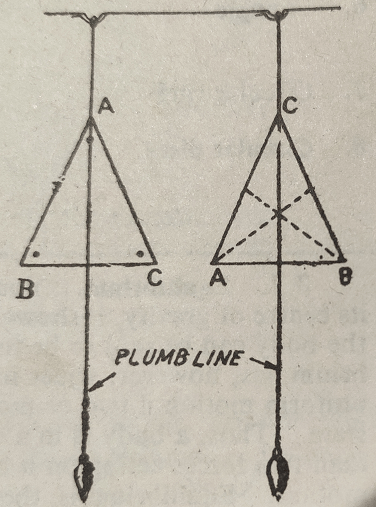
Experiment 1: Take a lamina and make three different holes on its different corners. Suspend it from its one hole (A) and also drop a plumb line from the point of support as shown. Let both lamina and plumb line come to rest. Draw a line to mark the position of the plumb line along the lamina. Now suspend the lamina from its another hole (B) and proceed as in the first case. The point of intersection of two lines, thus obtained, is the centre of gravity of lamina. Now if the lamina is suspended from its third hole (C), the line drawn to mark the position of the plumb line along the lamina, in this case, will pass through the same point which is the centre of gravity of lamina.
Experiment 2: Take a metre rod and place it on the edge of a wedge at its different positions. The point at which the metre rod is balanced is the point at which its centre of gravity lies. This may be further verified by balancing the metre rod on a needle.
When a body has a regular geometrical shape with its mass distributed uniformly throughout, its centre of gravity is always situated at its geometrical centre. The centre of gravity of such a body can be found very easily.
The centre of gravity of regular bodies can be determined by balancing method and the centre of gravity of irregular bodies can be obtained by the plumb line method.
| Body | Position of centre of Gravity |
|---|---|
| Uniformly thick rod | Middle point |
| Square | Point of intersection of its diagonals |
| Rhombus | Point of intersection of its diagonals |
| Parallelogram | Point of intersection of its diagonals |
| Sphere | At its centre |
| Triangle | At the point of intersection of its median |
| Circular ring | At its mid-point (outside the body) |
| Circular disc | At the middle point of the line joining the mid-points of the two circular faces |
- Flotation of Bodies
- Relative Density and Specific Gravity
- Buoyancy And Archimedes Principle
- Newtons First Law Of Motion
- Newtons Second Law of Motion
- Newtons Third Law of Motion
- Electrochemistry Notes From Tamil Board
Comments (No)