Inverse of a Function:
Consider a one-one onto function, f: x → y and let y be any arbitrary element of Y. Since f is onto, there exists at least one element x ∈ X such that f(x) = y. Again, as f is one-one, the element x ∈ X is unique. So corresponding to every element y ∈ Y, there exists a unique element x ∈ X and we can define a function g from Y to X i.e., g: Y → X such that g(y) = x for all y ∈ Y. This function g, associated with the function f, is known as the inverse of f and is denoted by f-1.
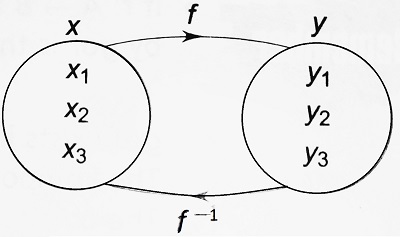
Thus, if f: X → Y be one-one onto function and if f(x) = y, where x ∈ X and y ∈ Y, then f-1: Y → X defined by f-1(y) = x is called the inverse of the function f(x).
A function whose inverse exists is known as an invertible or an inversible function. Obviously, the domain of f-1 = range of f.
Properties of Invertible Functions:
- The inverse of a bijection is unique.
- The inverse of a bijection is also a bijection.
- If f: A → B and g: B → C are two bijections, then gof: A → C is a bijection, and (gof)-1 = f-1og-1.
- If f: A → B is a bijection and g: B → A is the inverse of f, then fog = IB and gof = IA, where IA and IB are identity functions on the sets A and B respectively.
- If f: A → B and g: B → A be two functions such that gof = IA and fog = IB, then f and g are bijections and g = f-1.
| Example- If f: R to R defined by f(x) = (3x + 7)/2 for all x ∈ R. Find f-1. Solution- f(x) = (3x + 7)/2 f is one-one: Let x1, x2 ∈ R (domain) such that f(x1) = f(x2) ⇒ (3x1 + 7)/2 = (3x2 + 7)/2 ⇒ 3x1 + 7 = 3x2 + 7 ⇒ 3x1 = 3x2 ⇒ x1 = x2 ∴ f is one-one. f is onto: Let y ∈ R (codomain) such that f(x) = y ⇒ (3x + 7)/2 = y ⇒ 3x = 2y – 7 ⇒ x = (2y-7)/3 ∴ f is an on-to function. Since f is one-one as well as onto, so the inverse of f exists. Inverse of f: Let f(x) = y ⇒ (3x + 7)/2 = y ⇒ 3x = 2y – 7 ⇒ x = (2y – 7)/3 ⇒ f-1(y) = (2x – 7)/3 ∴ Inverse is (2x – 7)/3 |
| Example- If f: A → B be given by f(x) = 2x + 1 and A = {1, 3, 5}, B = {3, 7, 11}, then write f and f-1 as sets of ordered pairs. Solution- f(x) = 2x + 1 Now, f(1) = 2(1) + 1 = 3 f(3) = 2(3) + 1 = 7 f(5) = 2(5) + 1 = 11 ∴ f = {(1, 3) (3, 7) (5, 11)} and f-1 = {(3, 1) (7, 3) (11, 5)} |
| Example- If f: R → R is defined by f(x) = x3 – 2 for all x ∈ R, show that f is a bijection. Find f-1(x) and f-1(3). Solution- f is one-one: Let x1, x2 ∈ R (domain) such that f(x1) = f(x2) ⇒ x13 – 2 = x23 – 2 ⇒ x13 = x23 ⇒ x1 = x2 ∴ f is one-one. f is onto: Let y ∈ R (codomain) such that f(x) = y ⇒ x3 – 2 = y ⇒ x3 = y + 2 ⇒ x = (y + 2)1/3 For all values of y ∈ R, x ∈ R (domain). ∴ f is an on-to function. Since f is one-one as well as onto. ∴ f is a bijection and hence invertible. Inverse of f: Let y ∈ R such that, f(x) = y ⇒ x3 – 2 = y ⇒ x3 = y + 2 ⇒ x = (y + 2)1/3 ⇒ f-1(y) = (y + 2)1/3 ∴ Inverse of f(x) is f-1(x) = (x + 2)1/3 Now, f-1(-3) = (-3 + 2)1/3 = (-1)1/3 = -1 |









Comments (No)